Элементарные булевы функции. Равносильности

Булевых (или логических) функций от одной переменной 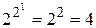. Они приведены в следующей таблице:

			отрицание

Основные элементарные булевы функции от двух переменных приведены в следующей таблице:

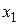
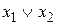
		конъюнк- ция	дизъюнк- ция	имплика- ция	эквивален-тность	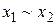сложение по модулю два	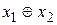стрелка Пирса	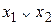штрих Шеффера

Функция называется конъюнкцией, ее обозначают также 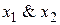, но чаще всего знак конъюнкции аналогично знаку умножения опускают и пишут 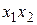. Конъюнкция 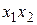равна единице, только есл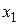и =1 и =1 одновременно, поэтому ее часто называют функцией И. Еще одно название конъюнкции ― логическое умножение, поскольку ее таблица истинности действительно совпадает с таблицей обычного умножения для чисел 0 и 1.

Функция 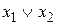называется дизъюнкцией. Дизъюнкция 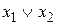равна единице, только если 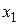=1 или =1 (т.е. хотя бы одна переменная равна единице), поэтому ее часто называют функцией ИЛИ.

Кроме таблицы истинности, булевы функции могут быть заданы аналитически с помощью формул. Например, .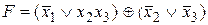

Если формула a реализует булеву функцию F,которая тождественно равна единице, то она называется тождественно истинной. Если формула a реализует булеву функцию F, которая тождественно равна нулю, то она называется тождественно ложной.

Если формулы a и b зависят от одних и тех же переменных и реализуют одну и ту же булеву функцию F,то формулы a и b называются равносильными.