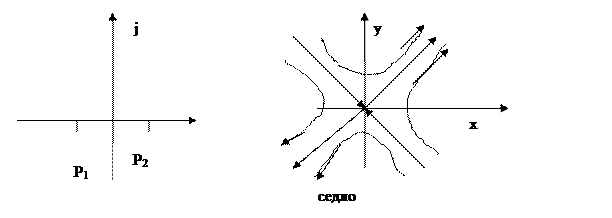
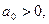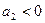Для изучения процессов в САУ введем понятие фазового пространства системы. Для этого уравнения САУ представим в форме Коши:
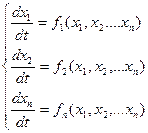
При 
- ненулевые начальные условия: 
.
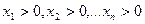При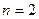 
фазовое пространство вырождается в фазовую плоскость с координатам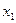и 
и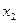 
.
n=3 Трехмерное фазовое пространство
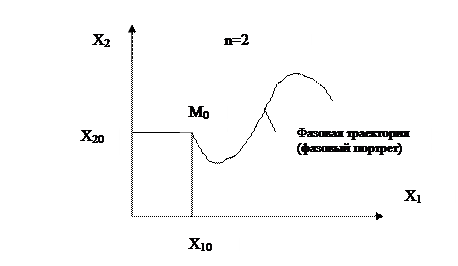
САУ удобно исследовать на фазовой плоскости , но для этого их надо упрощать до дифференциального уравнения второго порядка путем пренебрежения параметрами и выбора двух наиболее существенных фазовых координат.
Рассмотрим фазовые траектории САУ второго порядка.
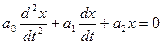(1) 
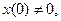
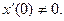
Сделаем подстановку
(2)
Тогда
. (3)
Учтем, что из (2)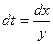 
Тогда (3) перепишется
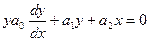
и уравнение фазовых траекторий примут вид:
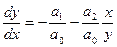
На фазовой плоскости точка
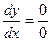находится в начале координат и является точкой установившегося состояния или особой точкой.
Точка называется особой, так как через нее проходит множество траекторий ( к установившемуся состоянию можно придти путем многих переходных процессов)
Если фазовый портрет входит в эту точку , то установившееся состояние устойчивое, если выходит –неустойчивое.
Связь фазовых траекторий и переходных процессов.
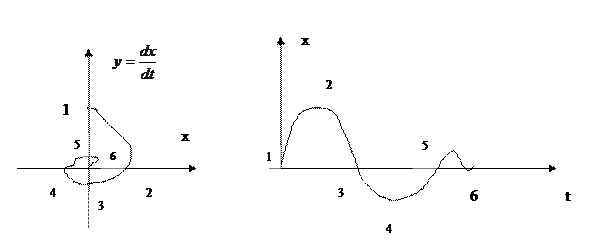
Рассмотрим фазовые траектории САУ второго порядка при различных его параметрах, т.е. при разных корнях характеристического уравнения.
Характеристическое уравнение, соответствующее дифференциальному уравнению (1):
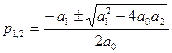
1. 
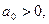
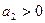
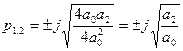
2. . 
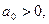
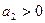
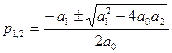
При этом соотношения коэффициентов таково, что 
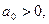
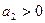
3.
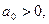
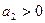
Соотношение параметров таково, что корни – вещественные.
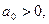
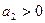
4. 
