|
|
ПаскальСиАссемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации |
Основные определенияДата добавления: 2014-06-06; просмотров: 1094; Нарушение авторских прав
|
Уроки php mysql Программирование Онлайн система счисления Калькулятор онлайн обычный Инженерный калькулятор онлайн Замена русских букв на английские для вебмастеров Замена русских букв на английские
Аппаратное и программное обеспечение
Графика и компьютерная сфера
Интегрированная геоинформационная система
Интернет
Компьютер
Комплектующие компьютера
Лекции
Методы и средства измерений неэлектрических величин
Обслуживание компьютерных и периферийных устройств
Операционные системы
Параллельное программирование
Проектирование электронных средств
Периферийные устройства
Полезные ресурсы для программистов
Программы для программистов
Статьи для программистов
Cтруктура и организация данных
| |||||||||
|
Не нашли то, что искали? Google вам в помощь! |
© life-prog.ru При использовании материалов прямая ссылка на сайт обязательна. |

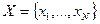 - множество возможных исходов (будем рассматривать денежные исходы). Простой лотереей будем называть набор вероятностей
- множество возможных исходов (будем рассматривать денежные исходы). Простой лотереей будем называть набор вероятностей 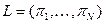 , где
, где  – вероятность исхода
– вероятность исхода 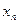 и
и  . Обозначим множество простых лотерей через
. Обозначим множество простых лотерей через 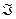 .
. таким образом, что для любых двух лотерей
таким образом, что для любых двух лотерей 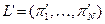 из множества простых лотерей:
из множества простых лотерей: 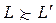 равносильно
равносильно 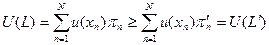 .
.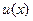 , определенную на денежных суммах, принято называть элементарной функцией полезности или функцией полезности Бернулли (будем считать ее непрерывной и возрастающей).
, определенную на денежных суммах, принято называть элементарной функцией полезности или функцией полезности Бернулли (будем считать ее непрерывной и возрастающей).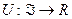 – функция ожидаемой полезности, представляющая предпочтения, определенные на
– функция ожидаемой полезности, представляющая предпочтения, определенные на 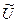 - другая функция ожидаемой полезности, отражающая те же предпочтения на
- другая функция ожидаемой полезности, отражающая те же предпочтения на 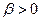 и
и 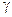 такие, что
такие, что 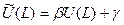 для любой лотереи
для любой лотереи  .
.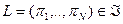 для него не лучше ожидаемого выигрыша этой лотереи,
для него не лучше ожидаемого выигрыша этой лотереи, 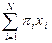 , полученного с определенностью. Если потребитель строго предпочитает ожидаемый выигрыш самой лотерее, то говорят, что он строго несклонен к риску или рискофоб.
, полученного с определенностью. Если потребитель строго предпочитает ожидаемый выигрыш самой лотерее, то говорят, что он строго несклонен к риску или рискофоб.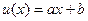 , где
, где 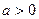 , или
, или 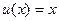 .
.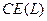 (полученную с определенностью), которая приносит индивиду такую же полезность, что и данная лотерея:
(полученную с определенностью), которая приносит индивиду такую же полезность, что и данная лотерея: 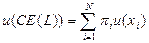 .
.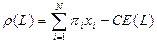 .
. (т.е. он любую лотерею оценивает в сумму меньшую ее ожидаемого выигрыша).
(т.е. он любую лотерею оценивает в сумму меньшую ее ожидаемого выигрыша). , однако существует возможность потери части этого богатства равной
, однако существует возможность потери части этого богатства равной 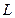 ,
, 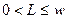 , в результате некоторого несчастного случая, вероятность которого равна
, в результате некоторого несчастного случая, вероятность которого равна 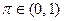 . Индивид может приобрести страховку от несчастного случая у нейтральной к риску страховой компании, не несущей операционных издержек, по цене
. Индивид может приобрести страховку от несчастного случая у нейтральной к риску страховой компании, не несущей операционных издержек, по цене 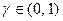 ). Пусть
). Пусть 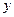 - это величина страхового покрытия приобретаемого индивидом, т.е. та сумма, на которую он страхуется. Будем считать, что страхование на сумму, превышающую потери, запрещено, т.е.
- это величина страхового покрытия приобретаемого индивидом, т.е. та сумма, на которую он страхуется. Будем считать, что страхование на сумму, превышающую потери, запрещено, т.е. 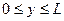 . Если индивид купит
. Если индивид купит  , а в противном случае –
, а в противном случае – 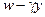 . Индивид выбирает такой объем страхового покрытия, который доставляет максимум ожидаемой полезности, т.е. является решением следующей задачи:
. Индивид выбирает такой объем страхового покрытия, который доставляет максимум ожидаемой полезности, т.е. является решением следующей задачи: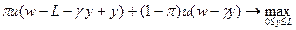
 , будем говорить, что условия страхования актуарно справедливы, а в случае
, будем говорить, что условия страхования актуарно справедливы, а в случае 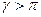 будем говорить, что страховка не является актуарно справедливой.
будем говорить, что страховка не является актуарно справедливой.