1. 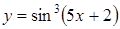
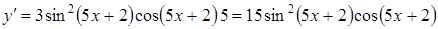 ,
,
2.  ,
,
3. 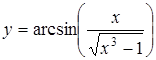 ,
,
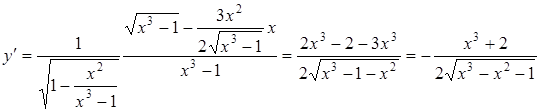 .
.
Дифференцирование неявно заданных функций
Если функция задана неявно, перед дифференцированием следует определиться, какую переменную считать аргументом. Пусть 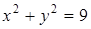 . Считаем
. Считаем 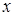 назависимой переменной,
назависимой переменной, 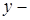 функцией. Можно из уравнения определить
функцией. Можно из уравнения определить 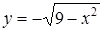 и
и 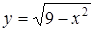 , тогда
, тогда 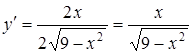 и
и  . Но можно поступить по-другому. Дифференцируем обе части уравнения
. Но можно поступить по-другому. Дифференцируем обе части уравнения 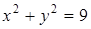 по переменной
по переменной 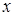 , используя при этом правило дифференцирования сложных функций
, используя при этом правило дифференцирования сложных функций 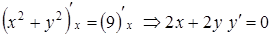 , откуда следует
, откуда следует  .
.
После подстановки в полученную формулу значения 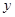 , естественно получаем те же формулы для производной.
, естественно получаем те же формулы для производной.
В рассмотренном случае из неявного задания функции можно было перейти к явному ее заданию. Иногда это невозможно, и приходится применять второй способ. Пусть
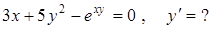 .
.
Отметим, что здесь уже задано, что 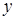 следует считать функцией
следует считать функцией 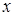 . Дифференцируем по
. Дифференцируем по 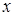 , считая
, считая 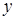 промежуточным аргументом
промежуточным аргументом
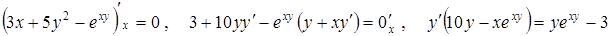
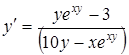 .
.
Дифференцирование функций, заданных параметрически
Ранее было получено для 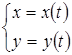 имеем
имеем 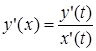 .
.
Пусть  ,
,
тогда 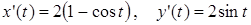 и
и 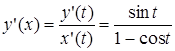 .
.
«Логарифмическое» дифференцирование
Здесь имеется ввиду дифференцирование с предварительным логарифмированием функции. Пусть  . При вычислении производной нет возможности использовать таблицу производных, так как эта функция не является ни степенной, ни показательной. Прологарифмируем обе части уравнения
. При вычислении производной нет возможности использовать таблицу производных, так как эта функция не является ни степенной, ни показательной. Прологарифмируем обе части уравнения 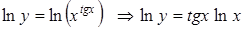 . В результате от явного задания функции перешли к неявному, при этом функция стала более удобной для дифференцирования. В самом деле
. В результате от явного задания функции перешли к неявному, при этом функция стала более удобной для дифференцирования. В самом деле 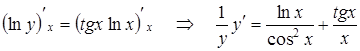 . В результате
. В результате
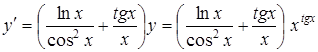 .
.