Непрерывная случайная величина, принимающая неотрицательные значения, имеет показательное распределение с параметром λ, если плотность распределения имеет вид: f(x)=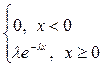 
, где λ-параметр, λ>0.
Кратко записывают так: X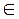 
Е(λ).
График плотности распределения выглядит следующим образом:
f(x)
λ 
0 x
Функция распределения показательно распределенной случайной величины такая:
F(x)=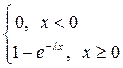 
F(x)
1
0 x
Вычислим числовые характеристики показательно распределенной с.в.
МX=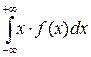 
= 
0- 
.
МX=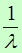 
DX=MX2-(МX)2=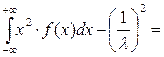
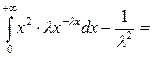
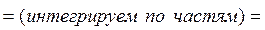
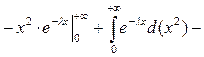
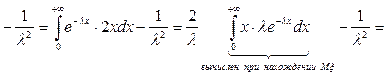
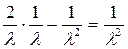
То есть DX=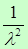 
Пример. Функция распределения времени (ч) безотказной работы радиоаппаратуры имеет вид:
F(x)=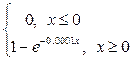 
Найти: 1. плотность распределения; 2. математическое ожидание.
Решение. 1. Параметр показательно распределенной с.в. равен λ=0,0001. Тогда плотность с. в. записывается следующим образом: f(x)= 
.
2. Математическое ожидание показательно распределенной с.в. вычисляется по формуле: МX=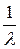 
= 
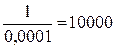(ч)
