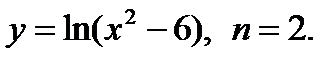Определение. Производной функции f(х) называется предел отношения приращения функции к приращению аргумента при ∆х стремящемся к нулю, если этот предел существует:
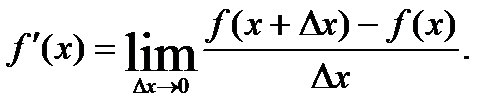
Производные простейших функций:
1. (  )' =
)' = 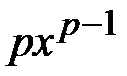 ; частные случаи:
; частные случаи: 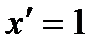 ; (
; ( 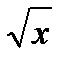 )' =
)' = 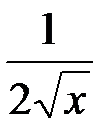 .
.
2. ( 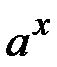 )' =
)' = 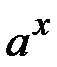
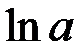 ; частный случай:
; частный случай: 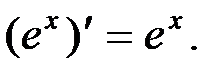
3. ( 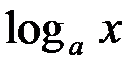 )' =
)' = 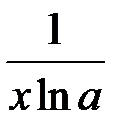 ; частный случай: (
; частный случай: ( 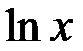 )' =
)' = 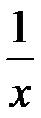 .
.
4. (sinx)' = cosx. 5. (cosx)' = − sinx.
6. (tgx)' = 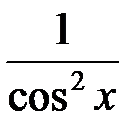 . 7. (ctgx)' =
. 7. (ctgx)' = 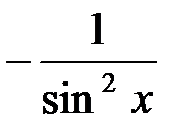 .
.
8. (arcsinx)' = 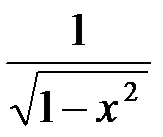 . 9. (arccosx)' = –
. 9. (arccosx)' = – 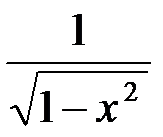 .
.
10. (arctgx)' = 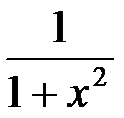 . 11. (arcctgx)' = –
. 11. (arcctgx)' = – 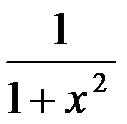 .
.
Правила дифференцирования
1. Производная постоянной: 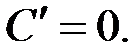
2. Производнаясуммы: 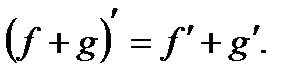
3. Производнаяпроизведения 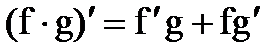 .
.
Следствие: 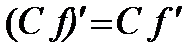 , т. е. постоянный множитель можно вынести за знак производной.
, т. е. постоянный множитель можно вынести за знак производной.
4. Производная частного: 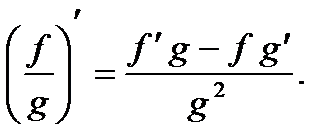
5. Производная сложной функции:  ,
,
где f = f(x), g = g(x) – дифференцируемые функции.
Пусть функция  заданапараметрически:
заданапараметрически: 
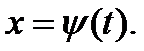 Тогда ее производная равна
Тогда ее производная равна
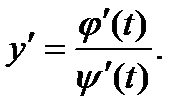
Примеры вычисления производных


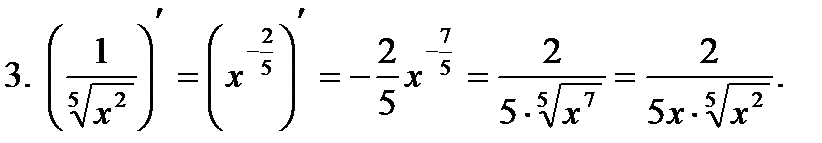
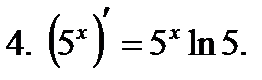

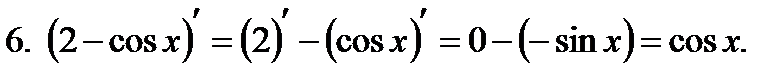
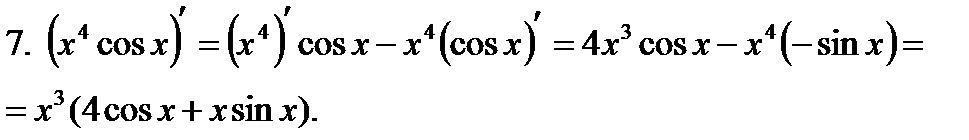
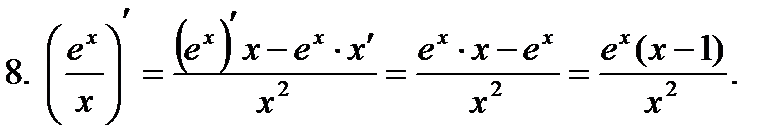
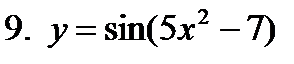 ,
, 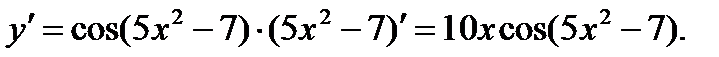
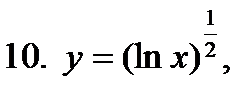
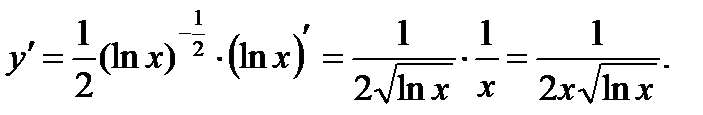
11. Найти производную функции, заданной неявно: 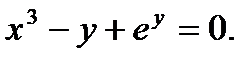
Решение.
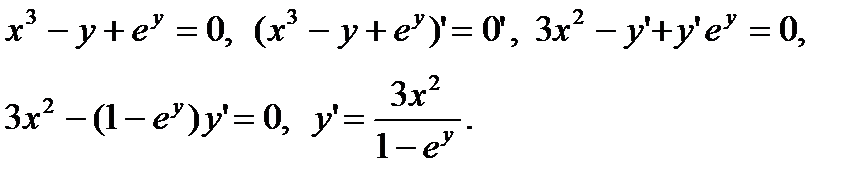
2.12. Найти производную функции по определению производной:
1) 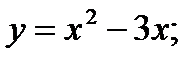 2)
2) 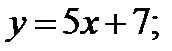 3)
3) 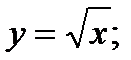
4) 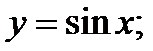 5)
5) 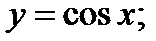 6)
6) 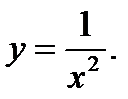
2.13. Найти производную функции:
1) 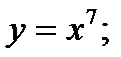 2)
2) 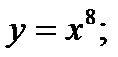 3)
3) 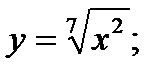 4)
4) 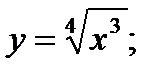
5) 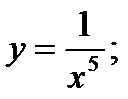 6)
6)  7)
7)  8)
8) 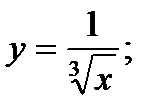
9) 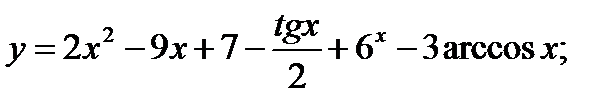
10) 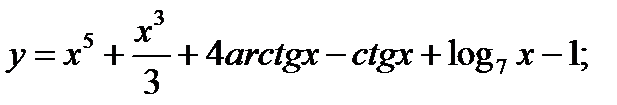
11) 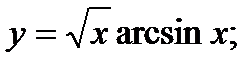 12)
12)  13)
13) 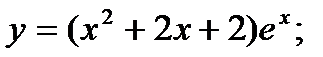
14) 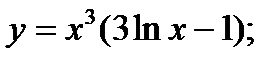 15)
15)  16)
16) 
17) 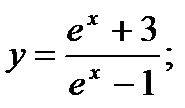 18)
18) 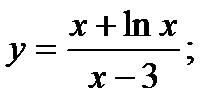 19)
19) 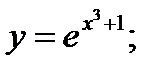
20) 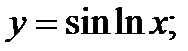 21)
21)  22)
22) 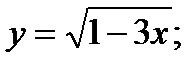
23) 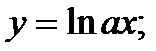 24)
24)  25)
25) 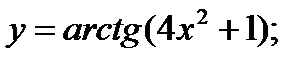 26)
26) 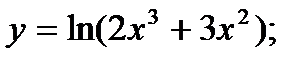 27)
27) 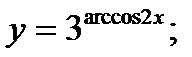 28)
28) 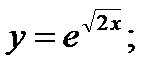
29) 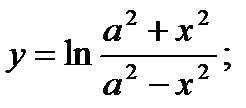 30)
30) 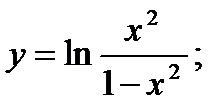 31)
31) 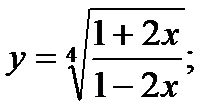
32) 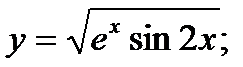 33)
33) 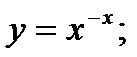 34)
34) 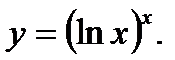
2.14. Найти производную функции и вычислить ее значение при x = x0:
1) 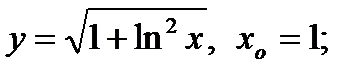 2)
2) 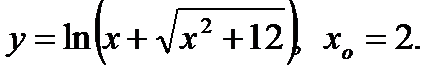
2.15. Найти производные функций, заданных неявно:
1) 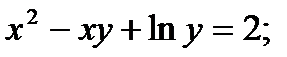 2)
2) 
3) 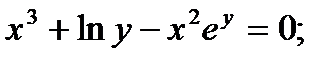 4)
4) 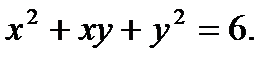
2.16. Найти производную n-го порядка функций:
1) 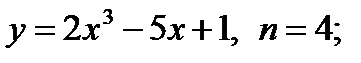 2)
2) 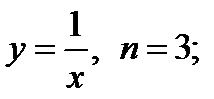
3) 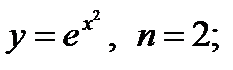 4)
4)