Ранее было показано, что значения эмпирической функции распределения в каждой точке можно рассматривать в качестве оценки значений в этой точке теоретической функции распределения, а различные выборочные моменты можно рассматривать как оценки соответствующих теоретических моментов. При этом в термин «оценка» вкладывался определенный асимптотический (при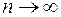 
) смысл: при большом объеме выборки 
значительная разница между эмпирическими (выборочными) и теоретическими характеристиками маловероятна.
Однако на практике, как правило, имею дело с ограниченным объемом выборки. Теория оценивания неизвестных параметров распределений посвящена обоснованию рекомендаций с точки зрения каких-либо критериев оптимальности для построения приближенных значений различных теоретических характеристик изучаемой модели и общие методы решения подобных задач.
Пусть имеется выборка 
, представляющая собой результат независимых наблюдений над некоторой случайной величиной 
с функцией распределения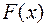 
. Предположим, что тип распределения генеральной совокупности известен, но зависит от неизвестного параметра 
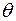(скалярного или векторного), то есть задана параметрическая статистическая модель наблюдений: 
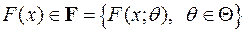. В общем случае задача оценивания формулируется так: используя информацию, доставляемую выборкой , сделать статистические выводы об истинном значении неизвестного параметра 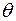, т.е. оценить параметр .
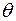Различают точечные и интервальные оценки неизвестных параметров.
