Применение тригонометрических подстановок для вычисления интегралов вида 
Для интегралов, не содержащих других иррациональностей, кроме квадратичного корня из квадратного трехчлена, применяются также тригонометрические подстановки, которые приводят интеграл от рациональной функции синуса и косинуса.
Чтобы применить эти подстановки, следует выполнить ряд преобразований. Из квадратного трехчлена, находящегося под корнем, надо выделить полный квадрат, после чего применить линейную подстановку. Это дает возможность получить под корнем следующие выражения:
1) при a>0 – сумму квадратов вида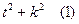 
.или 
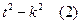. После того, как под корнем окажется выражение вида (1) для уничтожения иррациональности в подынтегральном выражении следует применить подстановку 
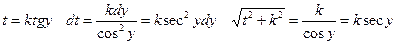. Если под корнем окажется выражение вида (2), то для уничтожения иррациональности в подынтегральном выражении надо применить подстановку 
2) при a<0 – выражения вида 
.или 
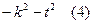. После того, как под корнем окажется выражение вида (3) для уничтожения иррациональности в подынтегральном выражении следует применить подстановку 
. Если под корнем окажется выражение вида (4), т.е. отрицательное выражение, по подстановки не применяются.
При решении интегралов используются следующие табличные интегралы:
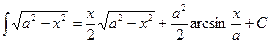
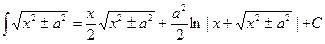
Примеры:
1)
2)
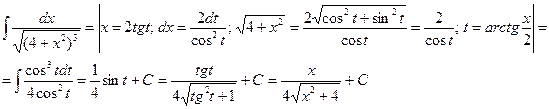
3)
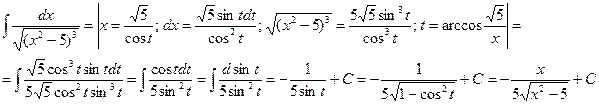
Лекция 6
