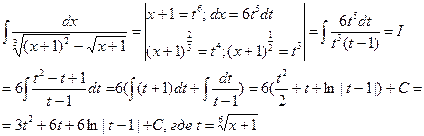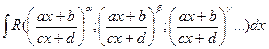Интегралы вида

,

где α, β, γ – дробно-рациональные числа.

Интегралы вычисляются постановкой 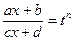, где n – наименьшее общее кратное знаменателей дробей α, β, γ. С помощью такой подстановки интеграл приводится к интегралу дробно-рациональной функции.

Частным случаем этого интеграла является интеграл с рациональной функций R от линейной функции (ax+b) c различными показателями. Тогда применяется подстановка .

Примеры.

1)

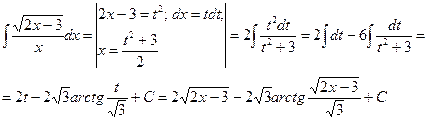
2)

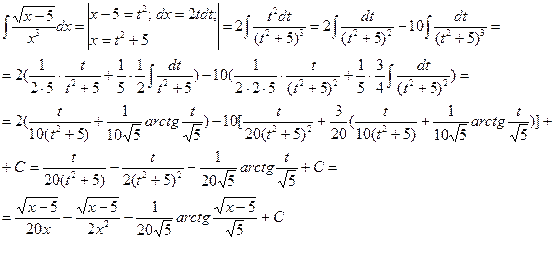
3)