Метод интегрирования по частям следует из формулы дифференциала произведения двух функций. Пусть u(x) и v(x) – две дифференцируемые функции переменной х. Тогда:
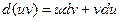. Проинтегрируем это выражение: 
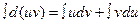. Но так как 
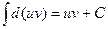, то:
(3.1)
Формула (3.1) называется формулой интегрирования по частям. Эту формулу применять целесообразно, когда интеграл правой части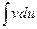 
более простой для вычисления, нежели исходный.
Приведем некоторые часто встречающиеся типы интегралов, вычисляемых этим методом.
I. Интегралы вида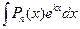 
; 
; 
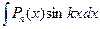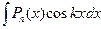, где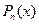 
- многочлен степени n, k – некоторое число. Чтобы найти эти интегралы, полагают 
, остальное принимают за dv, находят du и функцию v, интегрируя dv, и применяют формулу (3.1) n раз.
II. Интегралы вида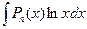 
; 
; 
; 
; 
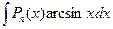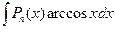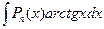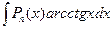. Эти интегралы находят, полагая 
, а оставшуюся функцию принимают за u.
III. Интегралы вида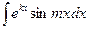 
; 
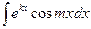, где m – некоторое число. За функцию u принимают 
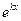, двукратно интегрируют по частям.
Примеры.
1)
2)
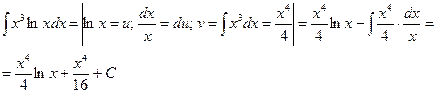
3)
,
