Задача численного дифференцирования состоит в приближенном вычислении производных функции u(x) по заданным в конечном числе точек значениям этой функции. Пусть на [a,b] введена сетка:
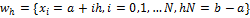 ,
,
И определены значения ui=u(xi) функции u(x) в точках сетки. В качестве приближенного значения u’(xi) можно взять, например, любое из следующих разностных отношений:

В качестве примера рассмотрим функцию
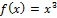 ,
,
для которой производная равна 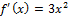 .
.
Код программы представлен в листинге 15.3.
Листинг 15.3. Приближенное вычисление производной
float a = 0;
float b = 3;
int m = 50;
float dx = (b - a) / m;
float x = 0, y = 0, yt = 0;
for (int i = 1; i <= m; i++)
{
x += dx;
y = (F3(x) - F3(x - dx)) / dx; // левая разность
yt = (F3(x + dx) - F3(x - dx)) / (2 * dx);
// центральная разность
g.DrawEllipse(Pens.Black,II(x)-2,JJ(y)-2, 4, 4);
g.DrawRectangle(Pens.Black,II(x)-2,JJ(yt)-2,4,4);
}
Результаты расчетов представлены на рис. 15.1.
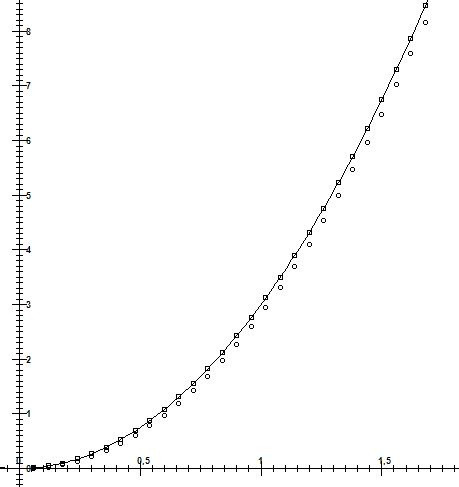
Рис. 15.1. Графики функций для расчетов
На графике видно, что производная, вычисленная через центральные разности (на рис. 15.1 изображена квадратами), хорошо совпадает с точным значением производной.