Пусть функция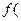 
) являетсястепенной функцией, умноженной на экспоненциальную функцию со степенью в виде линейной функции, т.е.
) = 
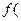
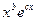. Имеем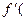 
) = 
, откуда определяются две конечные стационарные точки: = - 
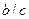и = 0 при 
. Вторая производная 
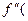
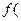
) от ) равна ) =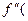 
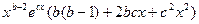и в стационарной точке = - 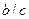равна - ) = -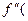 
(- 
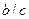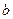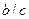
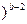, а в стационарной точке. = 0 при 
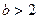
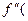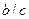- ) равна 0, при 
равна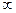 
. Поэтому необходимо рассмотреть только стационарную точку = - .
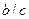Рассмотрим последовательно все возможные ситуации.
1. 
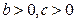
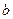принимает целочисленные конечные значения, 
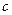принимает конечные значения. В этом случае 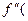- 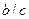) является конечным числом со знаком -, если 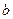- четное, и знаком +, если 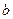- нечетное. Таким образом, если 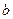- четное, то имеем максимум и, если 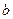- нечетное, то минимум. Если же 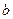принимает дробные конечные значения, то 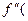- 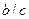) неопределенна, так как принимает комплексные значения.
2. 
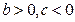. В этом случае 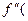- 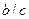) является конечным числом со знаком -, т.е. имеем максимум.
3. 
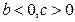. В этом случае 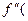- 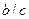) является конечным числом со знаком +, т.е. имеем минимум.
4. 
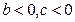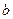, принимает целочисленные конечные значения. В этом случае 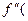- 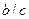) является конечным числом со знаком +, если 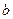- четное, и знаком -, если 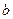- нечетное. Таким образом, если 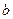- четное, то имеем минимум и, если 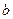- нечетное, то максимум. Если же 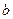принимает дробные конечные значения, то 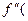- 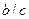) неопределенна, так как принимает комплексные значения.
