Ряд называется знакопеременным, если любой его член может быть, как положительным, так и отрицательным.
Рассмотрим знакочередующиеся ряды:
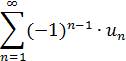
Теорема 1. Признак Лейбница (достаточный признак).
Если у знакочередующегося ряда
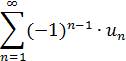
члены убывают по абсолютной величине, то есть  и
и
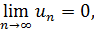
то ряд сходится, и его сумма не превосходит первого члена, то есть S≤ 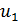 .
.
Пример.

Решение:
Применим признак Лейбница:

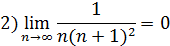
Следовательно, ряд сходится по Лейбницу.