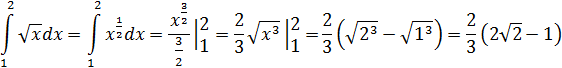1 тип.
Интегралы вида
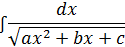
берутся выделением полного квадрата под корнем и сводятся к следующим табличным:
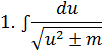
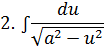
Пример 1:
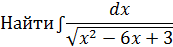
Решение:
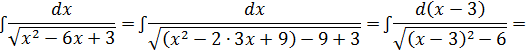
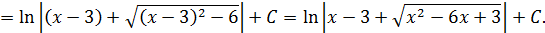
Пример 2:
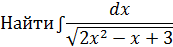
Решение:
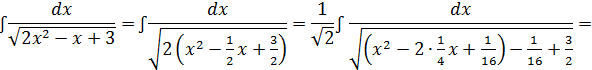
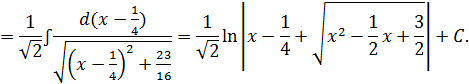
Тип.
Интегралы вида
берутся выделением в числителе производной от подкоренного выражения:
, при этом исходный интеграл разобьется на сумму двух интегралов.
Первый из них
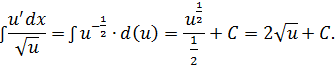
Второй интеграл относится к интегралам первого типа, рассмотренным выше.
Пример:
Решение:
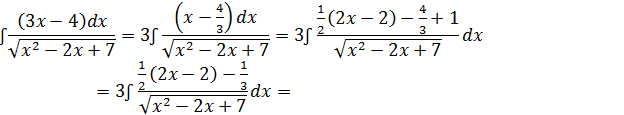
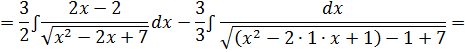
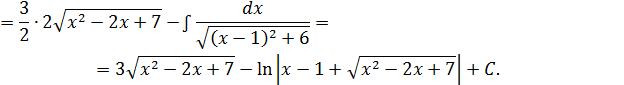
Лекция 11.ОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ. ФОРМУЛА НЬЮТОНА ‒ ЛЕЙБНИЦА.
Определенным интегралом от функции f(x)на промежутке[a;b] называется приращение первообразной функции F(x) при изменении аргумента от x = aдо x = b.
Обозначается
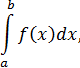
где a ‒ нижний предел интегрирования, а b‒верхний предел интегрирования.
Из определения следует:
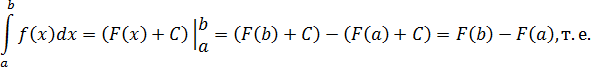
Пример.
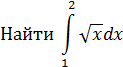
Решение:
