Лекция 4.ПРЕДЕЛ ФУНКЦИИ. Предел функции в точке и в бесконечности. Основные теоремы о пределах.Бесконечно малые и бесконечно большие функции.

Пусть функция y =f(x) определена в некоторойокрестностиx₀,кроме, может быть, самой точки x₀.

Определение.ЧислоA называется пределом функцииy =f(x) в точке x₀ (или при х →x₀), если для любого сколь угодно малого числа ε> 0найдетсятакоечисло δ> 0, что для всех х ¹x₀, удовлетворяющих неравенству

│ х –x₀│< δ, выполняется неравенство│f(x) –А│<ε.

Или кратко:

ε> 0 δ > 0, x:│ х –x₀│< δ, х ¹x₀=> │f(x) –А│<ε.

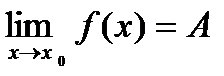
Геометрический смысл предела функции заключается в следующем: число 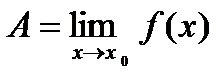, если для любой ε – окрестности точкиAнайдется такая δ – окрестность точки x₀, что для всех х ¹x₀ из этой окрестности соответствующие значения функции f(x) лежат в ε – окрестности точки А.

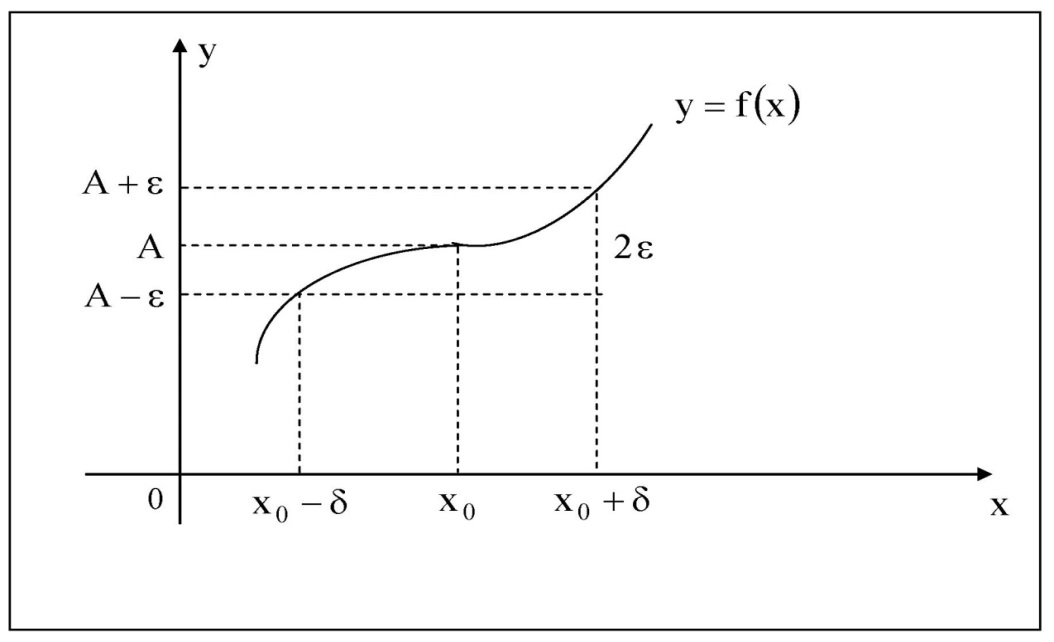
Рис. 1

Пример:Доказать, что

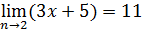
Решение. Возьмем произвольное 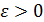и найдем такое, что для всех x, удовлетворяющих неравенству, , выполняется неравенство 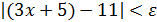, то есть .

Взяв , видим, что для всех x, удовлетворяющих неравенству, , выполняется неравенство 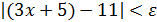, следовательно,

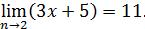
Пусть функция y =f(x) определена в промежутке (– ; + ).

Определение.ЧислоA называется пределом функцииf(x) при х , если для любого числа ε > 0существуеттакоечисло M = M (ε) > 0, что для всех значений x, удовлетворяющих неравенству │x│>M,выполняется неравенство │f(x) – А│< ε. В этом случае пишут f(x) = А.

Или кратко:

ε> 0 M> 0, │x│ >M=> │f(x) –А│<ε.

f(x) = А.