Предположим, что элементы матрицы вероятностей переходов P(t) дифференцируемы в интервале [0,+∞), причем под производной в нуле понимаем производную справа. Определим матрицу 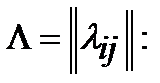

где P(s) - матрица переходных вероятностей, I - единичная матрица, с элементами

Величины λij называются инфинитезимальными коэффициентами, а Λ –инфинитезимальной матрицей. По другой терминологии λij - интенсивность (плотность) перехода цепи Маркова из состояния i в состояние j; λi = - λii - интенсивность (плотность) выхода из состояния i. По определению λij ≥ 0 для i ≠ j и λii < 0.
Очевидно, что 

Отсюда при s > 0 получаем
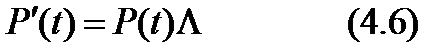
- прямое дифференциальное уравнение Колмогорова в матричной форме. Аналогичным образом из (4.2) получается и обратное дифференциальное уравнение Колмогорова в матричной форме

при этом P(0) = I. Каждое из уравнений (2.15) - (2.16) имеет единственное решение
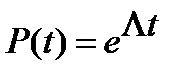
где через еΛt обозначена матричнозначная функция

В координатной форме уравнения (4.6) и (4.7) записываются в виде соответствующие систем дифференциальных уравнений Колмогорова

Из (4.3) аналогичными методами выводится система дифференциальных уравнений для вероятностей pi(t):
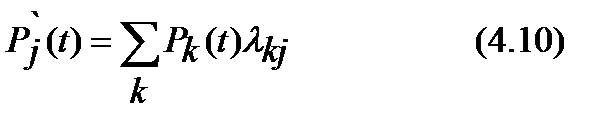
с начальным распределением рi (0) = Р{Х(0) = i}, i = 0,±1, ±2,... .