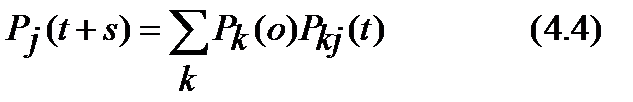Переходные вероятности Рij(t) удовлетворяют уравнению Колмогорова – Чепмена
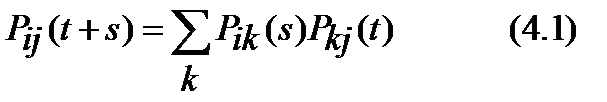
Это уравнение отражает тот факт, что марковская система, переходя из состояния i в состояние j за время t+s, сначала за время s из состояния i переходит в некоторое промежуточное состояние k, a затем за время t из состояния k переходит в состояние j, причем вероятность второго перехода не зависит от того, каким образом было достигнуто состояние k.
Докажем уравнение Колмогорова - Чепмена. С помощью формулы полной вероятности пишем
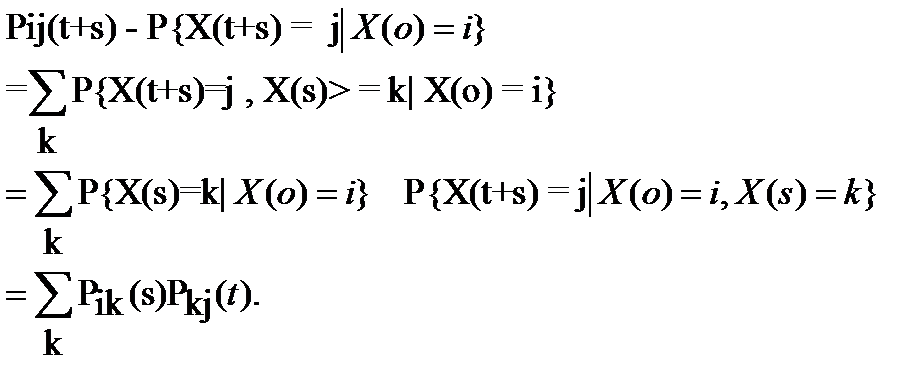
Здесь четвертое равенство написано на основании марковского свойства и свойства однородности процесса X(t). В матричной форме уравнение Колмогорова - Чепмена записывается как
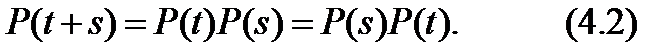
Для безусловных вероятностей состояний рj(t) = P{X(t) = j}, j = 0, ±1, ±2,... справедливо уравнение
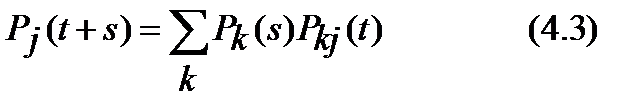
которое можно вывести из (4.1), если в (4.1) слева и справа умножить на рi (0) и затем просуммировать по всем индексам i = 0, ±1 , ±2 .... Если в (4.3) s = 0, то