Отдельные подсистемы или звенья

В операторном виде с учетом (5.19) уравнения системы можно записать в виде
A(p) X(p) = B(p) W(p) (5.42)
Y(p) = C(p) X(p) (5.43)
где X(p) - изображение по Лапласу переменной состояния, W(p) - входной и Y(p) - выходной переменных.
A(p) @ an pn + an-1pn-1 + .... + a1p + a0 многочлен от переменной р
B(p), C(p) - аналогичные многочлены ( (5.42) есть результат преобразования по Лапласу (5.17).
Из (5.42),(5.43) получаем
Y(p) = [C(p) B(p) / A(p)] W(p) (5.44)
Y(p) = H(p) W(p), H(p) = C(p) B(p) / A(p) (5.45)
Пусть система состоит из i = 1,2,...,n звеньев (подсистем)
Yi(p) = Hi(p) Wi(p), i =1,2,...,n (5.46)
Wi(p) =  (5.47)
(5.47)
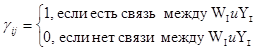
Wi' - внешние связи.
Для состояний уравнения получаются непосредственно из (5.42) Все состояния, обозначенные Xi(p), i = 1,2,...,n образуют вектор состояний системы. Выходы, не являющиеся входами других элементов данной системы, есть выходы системы. Входы элементов системы, не являющиеся выходами других элементов этой системы являются внешними входами. Входы и выходы могут быть как векторными, так и скалярными.
В общем случае система состоит множества элементов, соединенных между собой. Для анализа целесообразно эти элементы выделить в качестве отдельных звеньев, а потом объединить в одну систему. При всем кажущемся разнообразии соединений, фактически имеют место только 3 возможные схемы соединения элементов или звеньев.
Пусть число элементов равно 2.