Частотные характеристики линейных систем характеризуют реакцию объекта на гармонический сигнал. Основной частотной характеристикой является амплитудно-фазовая характеристика (АФХ). Рассмотрим преобразования Лапласа 
и Фурье 
.
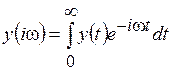При сравнении преобразований видно, что формально преобразование Фурье может быть получено из преобразования Лапласа простой заменой s на iω. Заменяя в уравнении (6.4) s на iω, получим
(an(iw)n+an−1(iw)n–1+...+a1(iw)+a0)y(iw)=(bm(iw)m+bm−1(iw)m–1+...+b1(iw)+b0)x(iw),
, (6.9)
.
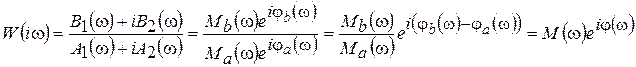Тогда амплитудно-частотная характеристика M(w) является четной функцией; фазочастотная характеристика j(w) – нечетной функцией; вещественная частотная характеристика Re(ω) – четной функцией; мнимая частотная характеристика Im(ω) – нечетной функцией (рис. 6.4 и 6.5).
Рис. 6.4 Свойство четности частотных характеристик: а) АЧХ; б) ВЧХ
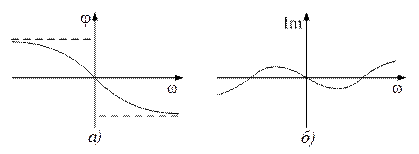
Рис. 6.5 Свойство нечетности частотных характеристик: а) ФЧХ; б) МЧХ
Амплитудно-фазовая характеристика также может рассматриваться как изображение Фурье от весовой функции
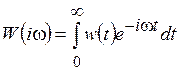. (6.10)
Так как e–iwt = coswt – isinwt, то из (6.10) определим вещественную и мнимую характеристики 
и, следовательно,
, 
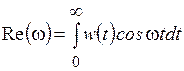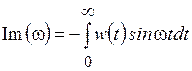. (6.11)
Откуда следует, что Re(ω) = Re(−ω), Im(ω) = −Im(−ω).
При практических расчетах АФХ строят только для положительных частот. Используя формулу обратного преобразования Фурье, можно по АФХ получить весовую характеристику
. (6.12)
