Метод Симпсона.

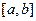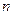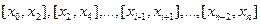Разобьем отрезок интегрирования на четное число равных частей с шагом . На каж­дом отрезке подынтегральную функцию 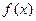заменим интерполяционным многочленом вто­рой степени:

.

Коэффициенты этих квадратных трехчленов мо­гут быть найдены из условий равенства много­члена в точках 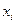соответствующим табличным данным 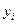.В качестве можно принять ин­терполяционный многочлен Лагранжа второй степени, проходящий через точки , : .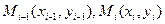

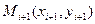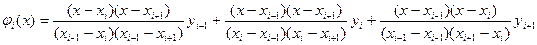Элементарная площадь может быть вычис­лена с помощью определенного интеграла. Учитывая равенства 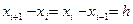, получаем . Проведя такие вычисления для каждого элементарного отрезка , просуммируем полученные выражения:

- формула Симпсона.

Блок-схема одного из простейших алгоритмов вычисления определенного интеграла по методу Симпсона представлена на рисунке. В качестве исходных данных задаются границы отрезка интегрирования , погрешность ,а также формула для вычисления значений подынтегральной функции 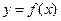. Первоначально от­резок 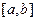разбивается на четыре части с шагом 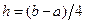. Вычисляется значение интеграла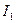. Потом число шагов удваивается, вычисляется значение с ша­гом . Условие окончания счета принимается в виде . Если это условие не выполнено, происходит новое деление шага пополам и т.д.

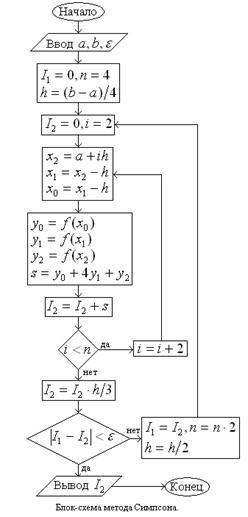Отметим, что представленный на рисунке алгоритм не является оптимальным. В частности, при вычислении каждого последующего приближения не используются значения функции 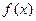, уже найденные на предыдущем этапе.