|
|
ПаскальСиАссемблерJavaMatlabPhpHtmlJavaScriptCSSC#DelphiТурбо Пролог1С Компьютерные сетиСистемное программное обеспечениеИнформационные технологииПрограммирование Linux Unix Алгоритмические языки Аналоговые и гибридные вычислительные устройства Архитектура микроконтроллеров Введение в разработку распределенных информационных систем Введение в численные методы Дискретная математика Информационное обслуживание пользователей Информация и моделирование в управлении производством Компьютерная графика Математическое и компьютерное моделирование Моделирование Нейрокомпьютеры Проектирование программ диагностики компьютерных систем и сетей Проектирование системных программ Системы счисления Теория статистики Теория оптимизации Уроки AutoCAD 3D Уроки базы данных Access Уроки Orcad Цифровые автоматы Шпаргалки по компьютеру Шпаргалки по программированию Экспертные системы Элементы теории информации |
Метод Ньютона (метод касательных).Дата добавления: 2014-03-21; просмотров: 6113; Нарушение авторских прав
|
Уроки php mysql Программирование Онлайн система счисления Калькулятор онлайн обычный Инженерный калькулятор онлайн Замена русских букв на английские для вебмастеров Замена русских букв на английские
Аппаратное и программное обеспечение
Графика и компьютерная сфера
Интегрированная геоинформационная система
Интернет
Компьютер
Комплектующие компьютера
Лекции
Методы и средства измерений неэлектрических величин
Обслуживание компьютерных и периферийных устройств
Операционные системы
Параллельное программирование
Проектирование электронных средств
Периферийные устройства
Полезные ресурсы для программистов
Программы для программистов
Статьи для программистов
Cтруктура и организация данных
| |||||||||
|
Не нашли то, что искали? Google вам в помощь! |
© life-prog.ru При использовании материалов прямая ссылка на сайт обязательна. |

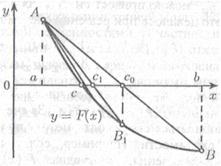 Пусть мы нашли отрезок
Пусть мы нашли отрезок 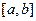 , на котором функция
, на котором функция 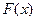 меняет знак. Для определенности примем
меняет знак. Для определенности примем 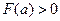 ,
, 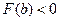 . В данном методе процесс итерации состоит в том, что в качестве приближений корню уравнения
. В данном методе процесс итерации состоит в том, что в качестве приближений корню уравнения 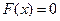 принимаются значения
принимаются значения 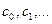 точек пересечения хорды с осью абсцисс.
точек пересечения хорды с осью абсцисс.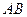 :
: 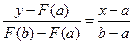 .
.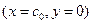 получим уравнение
получим уравнение  .
.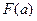 и
и  для рассматриваемого случая, приходим к выводу, что корень находится в интервале
для рассматриваемого случая, приходим к выводу, что корень находится в интервале  , т.к.
, т.к. 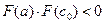 . Отрезок
. Отрезок 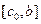 отбрасываем. Следующая итерация состоит в определении нового приближения
отбрасываем. Следующая итерация состоит в определении нового приближения 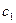 как точки пересечения хорды
как точки пересечения хорды 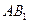 с осью абсцисс и т.д. Итерационный процесс продолжается до тех пор, пока значение
с осью абсцисс и т.д. Итерационный процесс продолжается до тех пор, пока значение 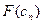 не станет по модулю меньше заданного числа
не станет по модулю меньше заданного числа  .
. Как видим, алгоритмы метода деления отрезка пополам и метода хорд похожи, однако второй из них в ряде случаев дает более быструю сходимость итерационного процесса. При этом успех его применения, как и в методе деления отрезка пополам, гарантирован.
Как видим, алгоритмы метода деления отрезка пополам и метода хорд похожи, однако второй из них в ряде случаев дает более быструю сходимость итерационного процесса. При этом успех его применения, как и в методе деления отрезка пополам, гарантирован.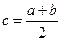 нужно использовать формулу
нужно использовать формулу 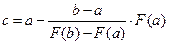 . Кроме того, в блок-схему необходимо ввести операторы вычисления значений
. Кроме того, в блок-схему необходимо ввести операторы вычисления значений  ойитерации вместо хорды проводится касательная к кривой
ойитерации вместо хорды проводится касательная к кривой 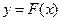 при
при 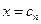 и ищется точка пересечения касательной с осью абсцисс. При этом не обязательно задавать отрезок
и ищется точка пересечения касательной с осью абсцисс. При этом не обязательно задавать отрезок 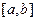 , содержащий корень уравнения
, содержащий корень уравнения 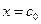 .
. Уравнение касательной, проведенной к кривой
Уравнение касательной, проведенной к кривой 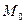 с координатами
с координатами 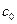 и
и  .
.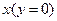 :
: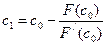 .
.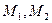 и т. д. Формула для
и т. д. Формула для  -гоприближения имеет вид :
-гоприближения имеет вид : 
 .
.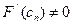 . Для окончания итерационного процесса могут быть использованы условия
. Для окончания итерационного процесса могут быть использованы условия 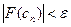 или условие близости двух последовательных приближений:
или условие близости двух последовательных приближений: 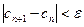 .
.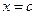 — корень уравнения
— корень уравнения 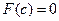 , а
, а 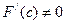 и
и  непрерывна. Тогда существует окрестность
непрерывна. Тогда существует окрестность 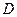 корня
корня 
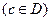 такая, что если начальное приближение
такая, что если начальное приближение 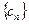 сходится к
сходится к 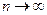 . При этом для погрешности корня
. При этом для погрешности корня 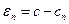 имеет местосоотношение :
имеет местосоотношение : .
.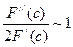 , то легко показать, что при
, то легко показать, что при 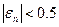 после пяти-шести итераций погрешность станет величиной порядка
после пяти-шести итераций погрешность станет величиной порядка  . Это наименьшее возможное значение погрешности при вычислениях на современных ЭВМ даже с удвоенной точностью. Заметим, что для получения столь малой погрешности в методе деления отрезка пополам потребовалось бы более 50 итераций.
. Это наименьшее возможное значение погрешности при вычислениях на современных ЭВМ даже с удвоенной точностью. Заметим, что для получения столь малой погрешности в методе деления отрезка пополам потребовалось бы более 50 итераций.