Тема 3. Общие положения планирования второго порядка

Проблема выбора правил автоматической остановки

Обычно задают требуемое количество реализаций или длины интервала моделирования. Другой способ задание доверительных интервалов оцениваемых величин и остановка прогона машинной модели по достижению этих интервалов. Наиболее эффективным способом в настоящее время является способ последовательного анализа. В последовательном анализе объем выборки не фиксируется, а после каждого i-го наблюдения принимается одно из следующих решений:

1. Принять данную гипотезу

2. Отвергнуть гипотезу

3. Продолжить испытания

Благодаря такому подходу объем выборки может быть уменьшен.

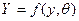Пусть распределение генеральной совокупности характеризуется функцией плотности вероятности . Задача состоит в оценке неизвестного параметра 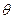. Определим нулевую и альтернативную гипотезы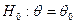

.

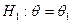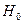Гипотезы проверяют на основании выборки нарастающего объёма m. Вероятность при условии, что - верна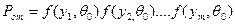

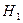Вероятность при условии, что - верна

.

Процедура проверки строится на отношении правдоподобия:

,

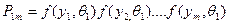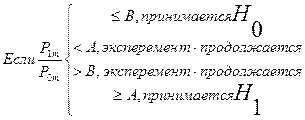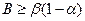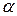где ; ; - ошибка первого рода – гипотеза верна, но отвергается; 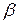- ошибка второго рода – гипотеза неверна, но принимается.

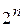Планы ПФЭ или ДФЭ 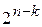позволяют найти коэффициенты, если аппроксимирующая поверхность хорошо описывает эксперимент полиномом без квадратичных членов (неполный квадратичный полином).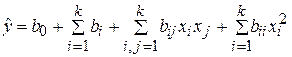

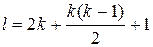Если ищется оптимальное значение функции отклика, то для около оптимальной области удается получить адекватную модель с помощью следующего полинома второго порядка:

Здесь k - число факторов; - число коэффициентов модели.

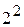Чтобы найти все коэффициенты, необходимо иметь план, в котором бы любой фактор варьировался бы не менее, чем на трёх уровнях. Так при k = 2, l = 6 план ПФЭ дает только 4 опыта, которых недостаточно для нахождения 6 коэффициентов. Если поставить эксперимент с 3 уровнями, то число опытов 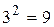, этого достаточно для определения всех коэффициентов.

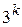Из-за быстрого роста объёма экспериментов ПФЭ невыгодны. Поэтому за основу принимают линейные планы, которые последовательно достраивают. Это предполагает реализацию опытов ПФЭ 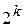, при k<5 или ДФЭ , при k>5 с добавлением некоторого количества специально расположенных точек. Такие планы называются центральными, композиционными планами (ЦКП).

Для двух факторов ЦКП второго порядка к ПФЭ (ядро плана) добавляются звёздные точки, отстоящие от центра на звёздное плечо и эксперименты в центре. Общее число опытов : .

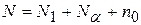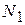- число опытов ядра 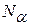или ; - число звездных точек 2k;

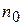- число опытов в центре плана. План имеет вид: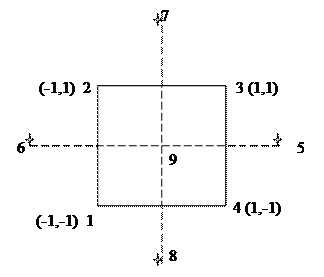

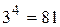
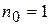
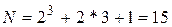
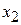
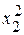
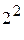
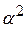
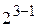Число уравнений варьирования каждого фактора равно пяти: (- α, - 1, 0, 1, α). Такое планирование требует значительно меньшего числа экспериментов по сравнению с ПФЭ .

Так, для k = 3 по ПФЭ

k = 4

Однако, для

Матрица ЦКП для 2 факторов:

							Части ЦКП
	+ + + +	- - + +	- + + -	+ - + -	+ + + +	+ + + +	ПФЭ
	+	+ α					Звездные точки
	+	- α
	+		+λ
	+		- λ
	+						Нулевая точка

В начале ставят опыты 1–4 составляющие ядро плана и позволяющие построить линейную модель. Если она оказывается неадекватной, то добавляют эксперименты в звездных точках (5–8 строки) и в центре эксперимента (строка 9). Это позволяет найти квадратичную модель почти стационарной области.

При трёх факторах можно сначала поставить ДФЭ . Если модель неадекватна, то перейти к ПФЭ 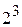. Если и в этом случае адекватность не достигается, то добавляют звездные точки (по осям) и опыт в центре. Величину звездного плеча и число опытов в центре плана выбирают так чтобы план эксперимента оставался ортогональным.