Введение в планирование эксперимента. Математический аспект

Измерение времени по особым состояниям

В этом случае системное время каждый раз изменяется на величину, строго соответствующую интервалам времени до момента очередного наступления события.

Для реализации моделирования по особым состояниям требуется планирование событий или разработка календаря. Календарь может быть задан в виде закона распространения интервалов между событиями или моменты наступления событий могут задаваться некоторым логическим условием, которое проверяется на каждом шаге моделирования.

Моделирование по особым состояниям целесообразно, если:

1. События распространяются во времени неравномерно или интервалы между ними велики.

2. Предъявляется повышение требования в точности определения взаимного расположения.

3. Необходимо учитывать наличие одновременных событий

Компоненты реальных систем могут характеризоваться величинами, которые измеряются в разных единицах времени. В этом случае они должны быть предварительно переведены к этому масштабу.

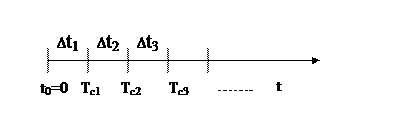
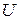Под экспериментом понимают создание некоторого комплекса условий , в результате которых могут наступать или не наступать события из некоторого заданного множества 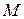и поэтому предметом теории эксперимента служит изучение отображения - комплекса условий на - множество результатов эксперимента. Если результат эксперимента зависит от случая, то эксперимент называют статистическим.

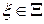Возможность планирования эксперимента обусловлена тем, что интересующий результат может быть получен при различном комплексе условий . Пусть - множество условий, которые может выбрать экспериментатор. Если множество 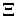не пусто, и стоимость эксперимента 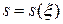– то такой эксперимент называется активным.

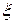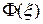Введём критерий качества эксперимента, который зависит от выбора , . Эта функция должна быть ограничена, например, снизу. Тогда

,

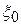где - план; - оптимальный план.

Многие экстремальные ситуации таковы, что нельзя обойтись одним критерием оптимальности, но можно указать множество критериев , каждый из которых желательно минимизировать выбором .

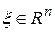Если является точкой n - мерного евклидова пространства и 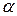принимает конечное число s Значений, то множество – (s-1)-мерное многообразие, определяемое как множество решений задачи

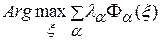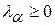, (1)

называется множеством Парето.

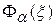Если часть не являются выпуклыми, то множество Парето будет содержать точки не являющиеся решением задачи (1). Линейная комбинация критериев , для выпуклых функций является компромиссным критерием. Другим компромиссным критерием может служить критерий 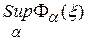Специфической задачей теории планирования эксперимента является конструирование критерия его оптимальности.

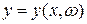Обычно экспериментатор до проведения эксперимента располагает сведениями об изучаемом явлении. Для применения математической теории требуется формализация этой информации. Пусть результатом эксперимента является реализация случайной функции , , где 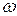- случайное событие. Если при фиксированных 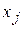, j=1,…N восстанавливается функция 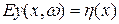, то такой эксперимент относят к числу регрессионных. Априорная информация состоит в указании множества F - функций, к которому принадлежит 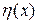. Наиболее простой случай параметрического задания 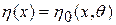Здесь – известная функция, а параметр 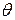из заданного параметрического множества - называют регрессионной моделью.

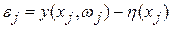Для подбора параметра необходимы также сведения о распределении ошибки Если совместное распределение 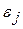известно также с точностью до параметра 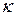. то задача определения 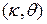– является параметрической задачей математической статистики. Параметр 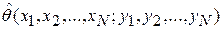. Оценивается с помощью статистики , параметр 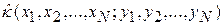оценивается с помощью статистики Оказывается, что погрешность зависит от выбора точек , в которых вычисляется функция y. Это даёт возможность построить критерий качества эксперимента и планировать эксперимент.