Элементы графов
Пусть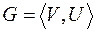 
- некоторый граф. Граф 
называется частичным графом графа 
, если 
, а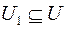 
. Граф 
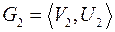называется подграфом графа (
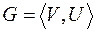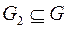), если: 1) 
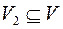; 2) из смежности в 
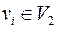и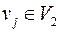 
следует смежность 
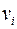и 
в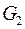 
. Граф 
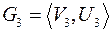называется частичным подграфом графа , если он является частичным графом подграфа графа .
Пусть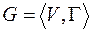 
- некоторый граф.
Степенью вершины называется величина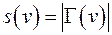 
- число дуг, инцидентных данной вершине. Степенью графа называется величина 
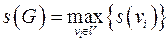. Минимальною степенью графа называется величина 
.
Пример
Теорема
Сумма степеней вершин графа есть число четное: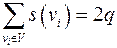 
.
Следствие
Число вершин с нечетными степенями – четно.
Граф называется регулярным, если степени всех его вершин равны.
Пример
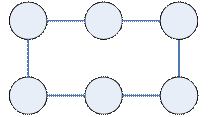
| Регулярный граф степени 2
|
Для орграфов:
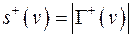- полустепень исхода.
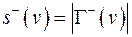- полустепень входа.
Теорема
Для любого орграфа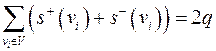 
.
Пример
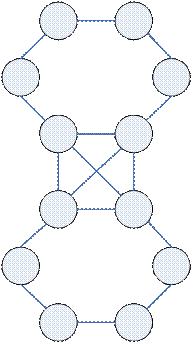
Распределение степеней вершин совпадает, но графы не изоморфны.
| 
|
