При вычислении пределов могут возникать некоторые неопределённости. Существуют специальные способы уйти от этих неопределённостей:
1. Раскрытие неопределённости 
, в этом случае числитель и знаменатель необходимо разложить на множители и сократить, пример:
.
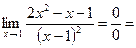
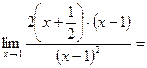
Иногда в случае неопределённости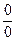 
можно и числитель, и знаменатель умножить на сопряжённое выражение для числителя или знаменателя.
.
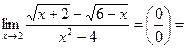
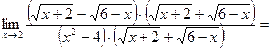
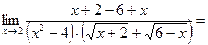
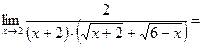
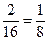2. Раскрытие неопределённости «бесконечность на бесконечность»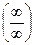 
.
В этом случае числитель и знаменатель необходимо разделить на наибольшую степень.
Пример:
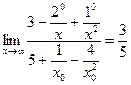
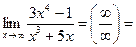
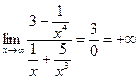
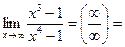
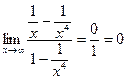
Таким образом, если числитель и знаменатель дроби многочлен, то предел дроби при 
равен:
1. Отношению коэффициентов при старших степенях, если старшая степень числителя равна старшей степени знаменателя;
2. Бесконечности, если старшая степень числителя больше старшей степени знаменателя;
3. Нулю, если старшая степень числителя меньше старшей степени знаменателя.
3. Раскрытие неопределённости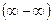 
.
В этом случае можно умножить на сопряжённое.
Пример:
.
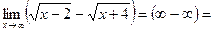
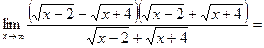
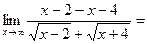
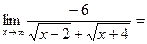
Иногда необходимо привести к общему знаменателю.
Пример: 
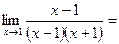
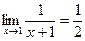
4. Раскрытие неопределенности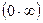 
.
.
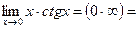
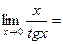
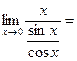
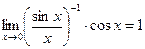5. Пределы, сводящие ко второму замечательному пределу.
.
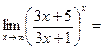
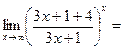
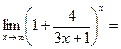
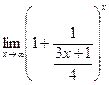
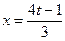
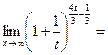
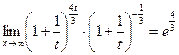