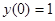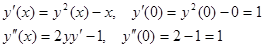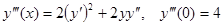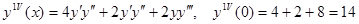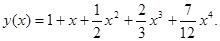1. Вычисление значений функций
Пример. Вычислить arctg 0.3 с точностью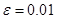 
.
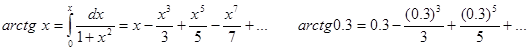
По следствию из признака Лейбница остаток числового знакочередующегося ряда оценивается модулем первого отброшенного члена.
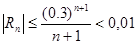. Из этого неравенства найдем n, n=2. 
.
Если разложение – знакопостоянный ряд, то надо подобрать какой-либо мажорантный ряд с известной суммой, например, оценить сверху члены ряда членами бесконечно убывающей геометрической прогрессии и оценку суммы ряда проводить по сумме прогрессии.
2. Вычисление интегралов.
Пример. Вычислить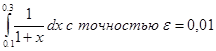 
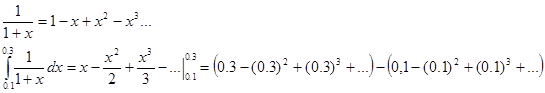
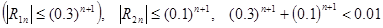
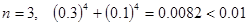
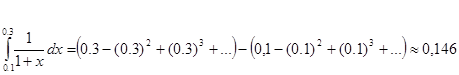
3. Решение дифференциальных уравнений.
Пример.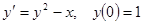 
1 способ. Представим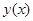 
в виде степенного ряда с неопределенными коэффициентами до 
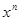(n – заранее определено). Это разложение подставляется в левую и правую часть, и приравниваются коэффициенты при равных степенях x. Решается система алгебраических уравнений и определяются коэффициенты.
.
Заметим, что при дифференцировании степень понижается на единицу, поэтому в разложении нужно запасать членов на k больше n, где k – порядок дифференциального уравнения.
Разложение проводится по степеням (x - x0), если начальные условия заданы в точке x0.
В данном уравнении производится разложение в ряд Маклорена, так как начальное условие задано в нуле.
.
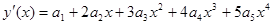Подставляем разложения в правую и левую части уравнения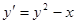 
.
= . 
.
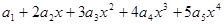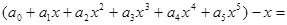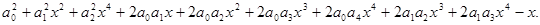
Удерживаем в разложении члены четвертых степеней, в коэффициентах при x5 будут
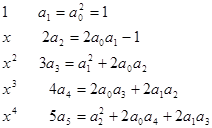
Отсюда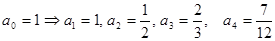 
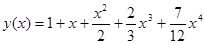
2 способ. Представим 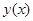в виде ряда Тейлора.
