Теорема о почленном интегрировании.
Теорема о почленном переходе к пределу.
Пусть 
ряд 
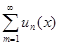равномерно сходится к S(x) в V, тогда
Тогда ряд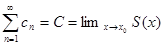 
(ряд из cn сходится к 
).
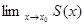(без доказательства).
Заметим, что суть теоремы содержится в формуле.
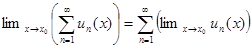, что и оправдывает название теоремы.
Пусть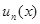 
непрерывны в V, пусть ряд 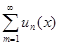равномерно сходится в V. Тогда ряд 
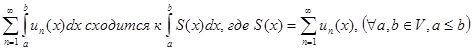, то есть функциональный ряд можно почленно интегрировать.
Заметим, что суть теоремы содержится в формуле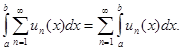 
Доказательство. Так как ряд 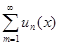равномерно сходится в V, то его сумма S(x) непрерывна (теорема о непрерывности суммы ряда) и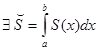 
Так как 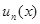непрерывны, то 
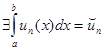. Составим ряд 
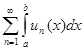, покажем, что он сходится к 
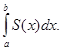Обозначим частичную сумму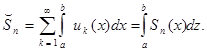 
Так как ряд 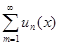равномерно сходится в V, то 
.
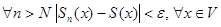Оценим 
.
Пусть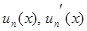 
непрерывны в V. Пусть ряд 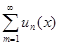сходится в V, а ряд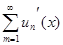 
.равномерно сходится в V. Тогда ряд 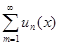можно почленно дифференцировать, причем (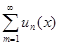
= .
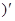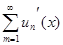Доказательство. Так как ряд 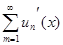сходится равномерно, то его сумма 
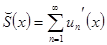- непрерывная функция (теорема о непрерывности суммы ряда). Ее можно интегрировать, применяя теорему о почленном интегрировании.
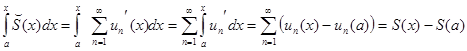
Дифференцируя, получим 
, то есть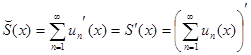 
.
