Свойства равномерно сходящихся функциональных рядов.
Признак Вейерштрасса равномерной сходимости ряда.
Пусть члены функционального ряда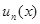 
можно мажорировать (ограничить по модулю) в области V членами сходящегося числового знакоположительного ряда, 
.
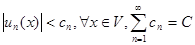Тогда функциональный ряд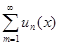 
равномерно сходится в области V.
Доказательство. Так как числовой ряд сходится, то для него выполнен критерий Коши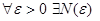 
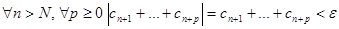(ряд знакоположителен, 
).
Тогда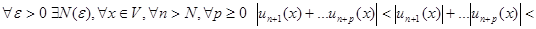 
.
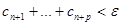Следовательно, выполнен критерий Коши равномерной сходимости ряда, и ряд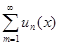 
сходится в области V равномерно.
Пример. Ряд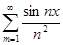 
сходится равномерно в R, так как 
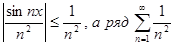- сходящийся числовой ряд.
Пусть члены 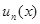функционального ряда 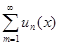- непрерывные функции в точке 
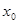- внутренней точке области V. Пусть ряд 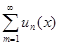сходится равномерно в области V. Тогда сумма функционального ряда – непрерывная функция в точке 
.
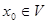Доказательство. Так как ряд сходится равномерно в V, то
.
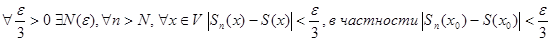Так как 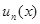- непрерывные функции в точке 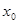, то и 
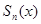непрерывна в 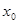как сумма конечного числа непрерывных функций.
Зафиксируем n>N. По непрерывности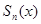 
.
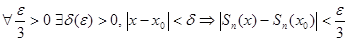Оценим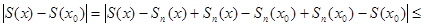 
.
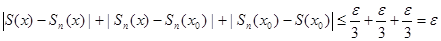Итак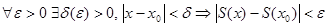 
, то есть сумма функционального ряда – непрерывная функция в точке .
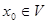