Экспонента
Гипербола
Нелинейная регрессия
Рассмотрим наиболее простые случаи нелинейной регрессии: гиперболу, экспоненту и параболу. При нахождении коэффициентов гиперболы и экспоненты используют прием приведения нелинейной регрессионной зависимости к линейному виду. Это позволяет использовать для вычисления коэффициентов функций регрессии формулы линейной зависимости.
При нахождении гиперболы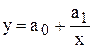 
вводят новую переменную 
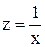, тогда уравнение гиперболы принимает линейный вид 
. После этого используют формулы для нахождений линейной функции, но вместо значений 
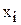используются значения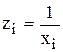 
; 
.
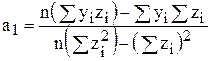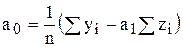Для приведения к линейному виду экспоненты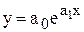 
проводят логарифмирование
;
;
.
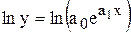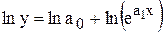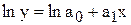Введя переменные 
и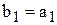 
, тогда 
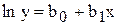, откуда следует, что можно применять формулы линейной зависимости, в которых вместо значений 
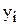надо использовать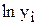 
; 
.
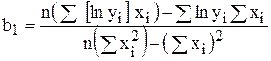При этом получаем численные значения коэффициентов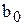 
и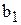 
, от которых надо перейти к 
и 
, и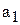спользуемых в модели экспоненты. Исходя из введенных обозначений и определения логарифма, получаем
, 
.
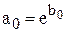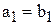Длянахождения коэффициентов параболы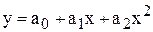 
необходимо решить линейную систему из трех уравнений
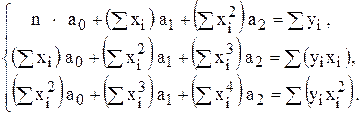
При вычислении коэффициента детерминации экспоненты все значения параметра Y (исходные, регрессионные, среднее) необходимо заменить на их логарифмы, например,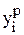 
– на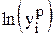 
и т.д.
