Используя локальную формулу Тейлора, можно доказать следующие утверждения.
4. Пусть функция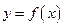 
дифференцируема 
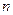раз в критической точке 
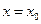и пусть при этом
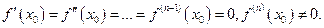
Тогда если 
то при 
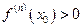в точке 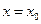функция 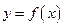достигает минимума; при 
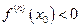функция 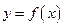достигает максимума в точке 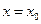.Если же
то в точке 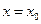функция 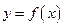не имеет локального экстремума.
5. Пусть функция 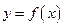трижды дифференцируема в точке 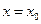и выполнены условия: а) 
б)
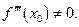Тогда 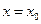–точка перегиба кривой 
Например, при исследовании функции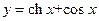 
на экстремум в точке 
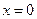исследовать знак производной 
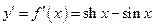довольно сложно. Так как
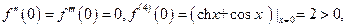
то (согласно утверждению 4) в точке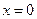функция 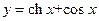достигает минимума.
Лекция 5. Первообразная и неопределенный интеграл. Свойства неопределенного интеграла. Таблица первообразных. Простейшие приемы интегрирования: подведение функции под знак дифференциала, выделение полного квадрата, замена переменных и интегрирование по частям в неопределенном интерале. Определенный интеграл, его свойства и геометрический смысл
Операция, обратная дифференцированию, называется интегрированием. Перейдем к ее изложению.
