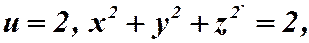End.
Определение: Если любой упорядоченной паре чисел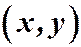 
из некоторого числового множества 
поставлено в соответствию по некоторому правилу f число z из множества Z, то говорят, что на множестве Dзадана функция 
.
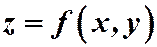х и у – независимые переменные (аргументы),
z – зависимая переменная (функция),
- область определения функции,
- множество значений функции.
Каждой упорядоченной паре чисел 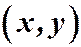соответствует единственная точка Мплоскости Оху.
Аналогично можно определить функцию любого конечного числа независимых переменных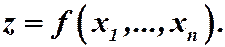 
Геометрическим изображениемфункции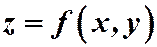в прямоугольной системе координат 
является некоторая поверхность.
Определение:Линией уровня 
функции 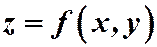называется линия на плоскости 
.
В каждой точке, лежащей на этой линии, функция 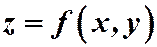принимает значение равное с.
Пример. Построить линии уровня функции для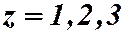 
.
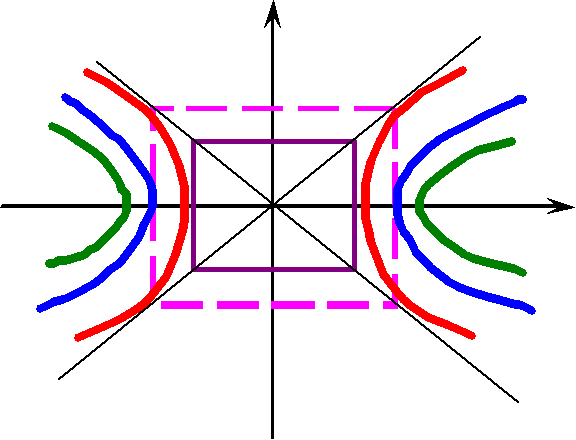
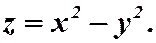
1) 
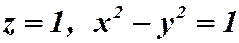- гипербола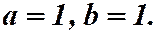 
2) 
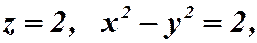
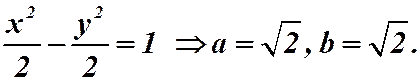
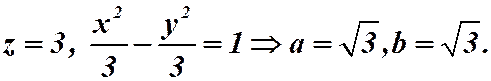
Определение: Поверхностью уровня называется поверхность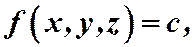 
в точках которой функция 
сохраняет значение, равное с.
Пример. Построить поверхности уровней для функци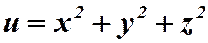и 
при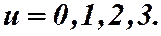 
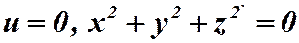- это точка,
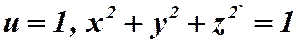- это сфера,
