Пример решения задачи ЛП с помощью МПУ
Шаг
Пример решения задачи ЛП с помощью МПУ
Пример решения задачи ЛП с помощью МПУ
Прямая задача А Двойственная задача А*
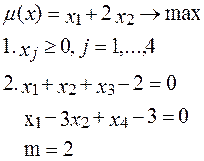
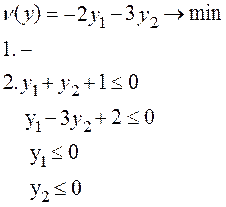
Найдем базис, базисное множество К, построим исходный допустимый вектор x(K)
|
| α1
| α2
| α3
| α4
| β
| y
|
|
|
|
|
| -2
| y1
|
|
| -3
|
|
| -3
| y2
|
| сj
|
|
|
|
|
|
|
Векторы α3, α4 – линейно независимы, базисное множество K={3,4}.
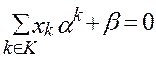 - имеет единственное решение - имеет единственное решение
| 
| Исходный допустимый вектор:
x(K)=(0,0,2,3); m=2
|
I. Определение вектора y(К).
Единственное решение имеет система: 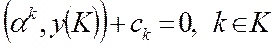 , K={3,4}.
, K={3,4}.

 y(K)=(0,0)
y(K)=(0,0)
II. Проверка двойственной допустимости ДБМ К
 ,
,  .
.
Проверим  , ,  ? ?
 Ясно, что Ясно, что 
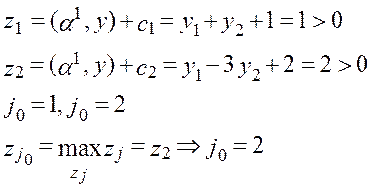
| Вектор
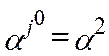 вводим в базис вводим в базис
|
III. Вычисление коэффициентов разложения вектора 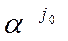 по базисным векторам.
по базисным векторам.
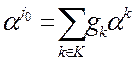 - разложение по базису
- разложение по базису
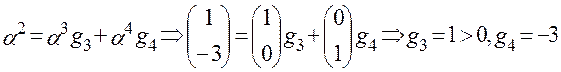
IV. Определение 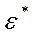 .
.
Определяем, какой вектор удалить из базиса.
 Т.к.
Т.к. 

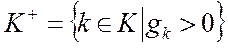 , К+ ={3}
, К+ ={3}

 Исключаем из базиса вектор
Исключаем из базиса вектор 