Двойственно допустимое базисное множество
Двойственно допустимое базисное множество
Задача А*.Минимизировать линейную функцию
на множестве m-мерных векторов
y = (y1, y2, . . ., ym),
удовлетворяющих системе линейных неравенств
1. -
2.  ,  .
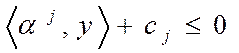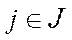| Для любого базисного множестваК единственное решение у(К) имеет система:
 , 
Если вектор у(К) является допустимым в двойственной задаче А* ( т. е. удовлетворяет условию2), то множество К называется двойственно допустимым базисным множеством (ДДБМ).
Обозначим через  ,  .
Если  ,  , то у(К) удовлетворяет условию2), то есть является допустимым вектором в двойственной задаче А*.
|
Итак, базисное множество является двойственно допустимым, если величины
, 
, (18)
удовлетворяют неравенствам
, 
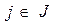(19)
Отметим, что величины (18) тесно связаны с коэффициентами разложения соответствующих векторов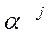 
по рассматриваемым базисным векторам, а именно:
, 
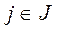, (20)
где 
- коэффициенты разложения векторов 
по рассматриваемому базису, т. е.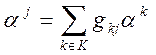 
. (21)
Действительно, учитывая (18), (21) , , и свойства скалярного произведения, получаем
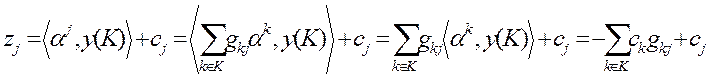. (22)
Каково бы ни было базисное множество K, для соответствующих векторов х(К) и у (К) имеет место равенство
.
Доказательство.Так как
, 
, 
, 
, 
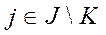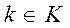получаем
,
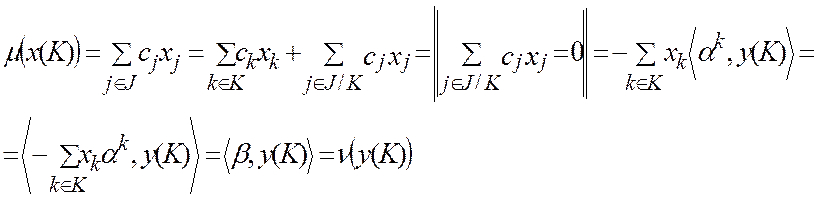что и требовалось показать.▄
