Двойственные задачи линейного программирования в канонической форме
Прямые задачи линейного программирования в канонической форме
| Общая форма ЛП
| 1 каноническая форма ЛП
| 2 каноническая форма ЛП
| Задача 1. Максимизировать линейную функцию
 на множестве векторов х=( х1,х2, …хn,),
удовлетворяющих условиям:
1. хj ³0 для jÎJ2
2.
на множестве векторов х=( х1,х2, …хn,),
удовлетворяющих условиям:
1. хj ³0 для jÎJ2
2. 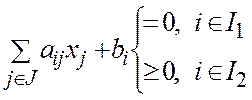
| Задача 2. Максимизировать функцию
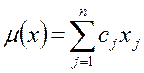 на множестве векторов
на множестве векторов 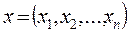 удовлетворяющих условиям
1. удовлетворяющих условиям
1.  2.
2. I2=I={1,2,…,m}
J2 J2 =J={1,2,…,n}
I2=I={1,2,…,m}
J2 J2 =J={1,2,…,n}
| Задача 3. Максимизировать функцию
 на множестве векторов
на множестве векторов  удовлетворяющих условиям:
1. удовлетворяющих условиям:
1.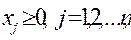 2.
2. I1=I={1,2,…,m}
J2 J2 =J={1,2,…,n}
I1=I={1,2,…,m}
J2 J2 =J={1,2,…,n}
| | Общая форма ЛП
| 1 каноническая форма ЛП
| 2 каноническая форма ЛП
| Задача 1*. Минимизировать линейную функцию
 на множестве векторов y=(y1,y2,…..ym),
удовлетворяющих условиям:
1. yi ≥ 0 для iÎI2
2. на множестве векторов y=(y1,y2,…..ym),
удовлетворяющих условиям:
1. yi ≥ 0 для iÎI2
2.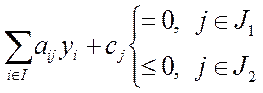
| Задача 2*. Минимизировать линейную функцию
 на множестве векторов
на множестве векторов 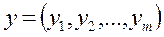 , удовлетворяет условиям 1. , удовлетворяет условиям 1.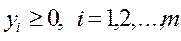 2.
2.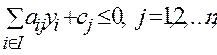
| Задача 3*. Минимизировать линейную функцию
 на множестве векторов
на множестве векторов 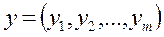 , удовлетворяет условиям
1. –
2. , удовлетворяет условиям
1. –
2. 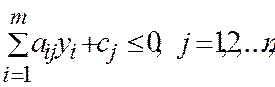
| | Для оптимальности допустимого вектора х=(х1,х2…,хn,) достаточно существование m-мерного вектора у=(у1,у2,…,уm), удовлетворяющего условиям:
| | Общая форма ЛП
| 1 каноническая форма ЛП
| 2 каноническая форма ЛП
| а) б)
б) 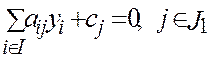 в)
в) 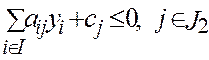 г)
г) д)
д)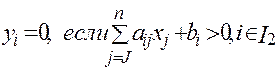
| а) б) –
в)
б) –
в) 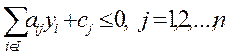
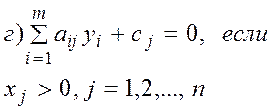

| а) –
б) –
в) 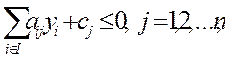
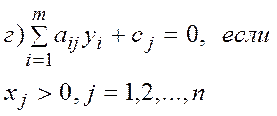 д) –
д) –
| Замечание. Наиболее удобной для решения задач ЛП является 2 каноническая форма
|