Фрактал Ньютона

Множество Жюлиа

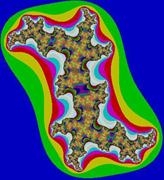
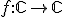Рассмотрим функцию . Множество Жюлиа определяется как граница множества точек , стремящихся к бесконечности при итерировании :

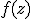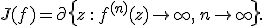
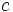Различные значения параметра могут порождать разнообразные множества Жюлиа, причем малейшее изменение этого параметра нередко приводит к существенным метаморфозам.

Формула итераций для фрактала Джулия такая:

z_k+1=z_k² + с ,

program J2; uses Graph, Crt; type TComplex = record X : Real; Y : Real; end; const iter = 50; max = 16; var z, t, c : TComplex; x, y, n : Integer; Cancel : Boolean; gd, gm : Integer; mx, my : Integer; begin Cancel := false; Randomize; gd := Detect; InitGraph(gd,gm,'c:\bp\bgi'); Mx := GetMaxX div 2; My := GetMaxY div 2; for y := -my to my do for x := -mx to mx do begin n := 0; z.x := x * 0.005; z.y := y * 0.005; c.x := 0.11; c.y := -0.66; while (sqr(z.x) + sqr(z.y) < max) and (n < iter) do begin t := z; {z^2 + c} z.x := sqr(t.x) - sqr(t.y) + c.x; z.y := 2*t.x*t.y + c.y; Inc(n); if keypressed then cancel := true; end; if n < iter then begin PutPixel(mx + x,my + y,16 - (n mod 16)); end; if cancel then exit; end; Readkey; CloseGraph;end.

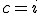При множество Жюлиа превращается в дендрит:

Другие формулы:

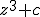
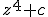
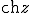
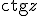
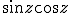
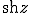
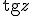
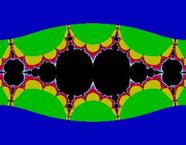
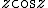
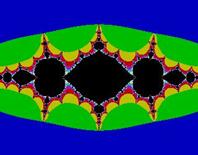
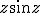
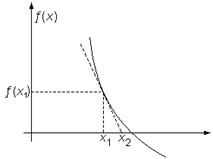
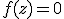Области с фрактальными границами появляются при приближенном нахождении корней нелинейного уравнения алгоритмом Ньютона на комплексной плоскости. Для функции действительной переменной метод Ньютона часто называют методом касательных. Поясним суть этого метода.

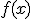Пусть нам задана функция , для которой известно приближенное значение ее корня 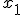, а также значение функции в этой точке 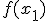и значение её первой производной 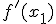. Тогда, проводя касательную к графику функции 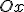в этой точке и определяя ее пересечение с осью , мы получим уточненное положение корня .

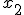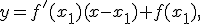
Т. к. уравнение касательной к в точке выглядит следующим образом:

то, приравнивая нулю, получаем, что уточненное значение корня 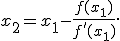связано с предыдущим значением соотношением

Беря теперь значение в качестве приближенного и повторяя эту процедуру, находим следующее приближение корня 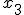и т. д. При некоторых условиях эта последовательность сходится к корню уравнения .

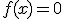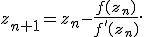
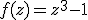Рассмотрим теперь комплексный случай. Рассмотрим уравнение и последовательность

Пусть . Как известно, это уравнение имеет три корня 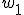, , 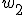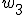. При выборе различных 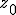процесс будет сходится к различным корням. Обозначим эти области притяжения через 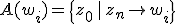. Артур Кэли поставил задачу описания областей 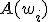. Оказывается границы этих областей имеют фрактальную структуру.

program N3;uses Graph, Crt;type Complex = Record x : Real; y : Real; end;const iter = 50; max = 1e+6; min = 1e-6; var z, t, d : Complex; p : Real; x, y, n : Integer; Cancel : Boolean; gd, gm : Integer; mx, my : Integer; begin Cancel := False; Randomize; gd := Detect; InitGraph(gd,gm,'c:\bp\bgi'); Mx := GetMaxX div 2; My := GetMaxY div 2; for y := -my to my do for x := -mx to mx do begin n := 0; z.x := X * 0.005; z.y := Y * 0.005; d := z; while (sqr(z.x)+sqr(z.y) < max) and (sqr(d.x)+sqr(d.y) > min) and (n < iter) do begin t := z; {z^3 - 1} p := sqr(sqr(t.x)+sqr(t.y)); z.x := 2/3*t.x + (sqr(t.x)-sqr(t.y))/(3*p); z.y := 2/3*t.y*(1-t.x/p);{} d.x := abs(t.x - z.x); d.y := abs(t.y - z.y); Inc(n); if keypressed then Cancel := true; end; PutPixel(mx + x,my + y,16 - (n mod 16)); if cancel then exit; end; Readkey; CloseGraph;end.

Существуют и другие примеры алгебраических фракталов, например, биоморфы, дерево Барнсли, лямбда-фрактал (вариант множеств Мандельброта и Жюлиа), горящий корабль, паук.