Теория алгоритмов ( англ. Theory of computation ) как отдельный раздел математики, изучающий общие свойства алгоритмов, возникла в 30-х годах 20 века. Алгоритмы, однако, прослеживаются в математике в течение всего времени ее существования. Необходимость точного математического уточнения интуитивного понятия алгоритма стала неизбежной после осознания невозможности существования алгоритмов решения многих массовых проблем, в первую очередь связанных с арифметикой и математической логикой (проблемы истинности арифметических формул и формул першопорядкового исчисления предикатов, 10-я проблема Гильберта о решении диофантовых уравнений и др.).. Для доказательства несуществования алгоритма надо иметь его точное математическое определение, поэтому после сформирования понятия алгоритма как новой и отдельной сущности первоочередной стала проблема нахождения адекватных формальных моделей алгоритма и исследования их свойств. При этом формальные модели были предложены как для первоначального понятия алгоритма, так и для производного понятия алгоритмически вычисляемой функции.
История развития теории алгоритмов
Впервые понятие алгоритма появилось в трудах Е. Бореля (1912) и Г. Вейля (1921).
Первыми формальными моделями алгоритмически исчисляемых функций были 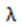 -обозначаемое функции ( Алонзо Черч, 1932) и загальнорекурсивни функции ( Курт Гедель, 1934). Указанные классы определялись как функции, графики которых порождаются соответственно исчислением
-обозначаемое функции ( Алонзо Черч, 1932) и загальнорекурсивни функции ( Курт Гедель, 1934). Указанные классы определялись как функции, графики которых порождаются соответственно исчислением 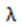 -конверсий и исчислением Ербрана-Геделя. В 1936 году Стивен Коул Клини распространил понятие загальнорекурсивнои функции на случай частичных функций, введя понятие частично рекурсивной функции, и описал класс таких функций в чисто функциональных терминах. В 1943 году Эмиль Пост предложил модель вычисляемых функций на основе введенного им исчисление специального вида ( канонических систем ).
-конверсий и исчислением Ербрана-Геделя. В 1936 году Стивен Коул Клини распространил понятие загальнорекурсивнои функции на случай частичных функций, введя понятие частично рекурсивной функции, и описал класс таких функций в чисто функциональных терминах. В 1943 году Эмиль Пост предложил модель вычисляемых функций на основе введенного им исчисление специального вида ( канонических систем ).
Для формализации самого понятия алгоритма были предложены точные математические описания алгоритмической машины и вычислимости на ней. Первой формальной моделью алгоритмической машины была машина Тьюринга ( Алан Тьюринг, Эмиль Пост, 1936). Из более поздних моделей отметим нормальные алгоритмы ( А. Марков, И952) и регистровые машины ( Д. Шепердсоном, Г. Стерджис, 1963).
В 1936 г. А. Черч и С. Клини доказали совпадение классов общеобразовательных рекурсивных и 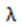 -означаемым функций. На основе этого факта и анализа идей, которые привели к указанным понятиям, А. Черч выдвинул тезис о совпадении класса АОФ с классом загальнорекурсивних функций. С. Клини обобщил этот тезис для случая частичных функций. Доказан А. Тьюрингом в 1937 г. совпадение классов частично рекурсивных функций и функций, вычисляемых на машинах Тьюринга, стало еще одним подтверждением тезиса Черча. Позже такие совпадения были установлены для всех известных формальных моделей АОФ. Поэтому есть все основания полагать, что каждая из названных выше формальных моделей адекватно уточняет интуитивное понятие АОФ.
-означаемым функций. На основе этого факта и анализа идей, которые привели к указанным понятиям, А. Черч выдвинул тезис о совпадении класса АОФ с классом загальнорекурсивних функций. С. Клини обобщил этот тезис для случая частичных функций. Доказан А. Тьюрингом в 1937 г. совпадение классов частично рекурсивных функций и функций, вычисляемых на машинах Тьюринга, стало еще одним подтверждением тезиса Черча. Позже такие совпадения были установлены для всех известных формальных моделей АОФ. Поэтому есть все основания полагать, что каждая из названных выше формальных моделей адекватно уточняет интуитивное понятие АОФ.
Теория алгоритмов возникла как раздел математической логики, понятия алгоритма тесно связано с понятием исчисления. Первые и самые многочисленные применения теория алгоритмов имеет именно в математической логике. Теория алгоритмов является теоретическим фундаментом программирования, она имеет применение везде, где встречаются алгоритмические проблемы (основы математики, теория информации, теория управления, конструктивный анализ, вычислительная математика, теория вероятности, лингвистика, экономика и др.)..
Основные понятия теории алгоритмов
Областью применимости алгоритма называется совокупность тех объектов, к которым его можно применить, то есть в применении к которым он дает результат. Об алгоритме U говорят, что он: 1) « вычисляет функцию f », когда его область применения совпадает с областью определения f, и U превращает любой х из своей области применения в f (х), 2) « решает множество A относительно множества X », когда он применяется к любому х из X, и превращает любой х из X 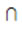 A на слово «да», а любое х из Х \ А - на слово «нет», 3 ) « перечисляет множество B », когда его область применения является натуральный ряд, а совокупность результатов есть B. Функция наз. вычислимой, если существует алгоритм, ее вычисляет. Множество называется разрешимой относительно X, если существует алгоритм, который решает ее относительно X. Множество наз.перечисляемых, если или она пустая, или существует перечисляя ее алгоритм.
A на слово «да», а любое х из Х \ А - на слово «нет», 3 ) « перечисляет множество B », когда его область применения является натуральный ряд, а совокупность результатов есть B. Функция наз. вычислимой, если существует алгоритм, ее вычисляет. Множество называется разрешимой относительно X, если существует алгоритм, который решает ее относительно X. Множество наз.перечисляемых, если или она пустая, или существует перечисляя ее алгоритм.
Детальный анализ понятия «алгоритм» обнаруживает, что (I) область возможных исходных данных и область применимости любого алгоритма является перечисляемых множествами. В свою очередь, (II) для любой пары вложенных одна в другую перечисляемых множеств можно подобрать алгоритм, у которого большая множество служит областью возможных исходных данных, а меньшее - областью применимости. Имеют место следующие основные теоремы: (III) функция f исчисляемое тогда и только тогда, когда перечисляемых ее график, то есть множество всех пар вида <х, f (x)>. (IV) Подмножество А перечисляемых множества X тогда и только тогда разрешима относительноX, когда А и X \ A перечисляемые. (V) Если А и В перечисляемые, то A объединить B и A 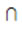 B также перечисляемые. (VI) В каждом бесконечном перечисляемые множестве X существует перечисляемые подмножество из неперераховуваним дополнением (в силу (IV) эта перечисляемые подмножество будет неразрешимым относительно X ). (VII) Для каждого бесконечного перечисляемых множества X существует исчисляемая функция, определенная на подмножестве этого множества и которая не продолжающееся до вычисляемой функции, определенной на всей X. Утверждение (VI) и (II) в совокупности дают пример алгоритма с неразрешимой областью применимости.
B также перечисляемые. (VI) В каждом бесконечном перечисляемые множестве X существует перечисляемые подмножество из неперераховуваним дополнением (в силу (IV) эта перечисляемые подмножество будет неразрешимым относительно X ). (VII) Для каждого бесконечного перечисляемых множества X существует исчисляемая функция, определенная на подмножестве этого множества и которая не продолжающееся до вычисляемой функции, определенной на всей X. Утверждение (VI) и (II) в совокупности дают пример алгоритма с неразрешимой областью применимости.
Разрешимы и перечисляемые множества составляют простейшие (и важные) примеры множеств, структура которых задается с помощью тех или иных алгоритмических процедур. Систематическое изучение множеств конструктивных объектов с точки зрения таких свойств этих множеств, которые связаны с наличием тех или иных алгоритмов, образует так называемую алгоритмическую теорию множеств.
Теорию алгоритмов можно разделить на дескриптивную (качественную) и метрическую (количественную). Первая исследует алгоритмы с точки зрения устанавливаемой ими соответствия между исходными данными и результатами; к ней относятся, в частности, проблемы построения алгоритма, что ему присущи те или иные свойства, - алгоритмические проблемы. Вторая исследует алгоритмы с точки зрения сложности как самих алгоритмов, так и вычислений, которыми задаются, т.е. процессов последовательного преобразования конструктивных объектов (см. сложности алгоритма ). Важно подчеркнуть, что как сложность алгоритмов, так и сложность вычислений могут определяться различными способами. Разработка методов оценки сложности алгоритмов и вычислений имеет важное теоретическое и практическое значение.
Применение теории алгоритмов
Во всех областях математики, в которых встречаются алгоритмические проблемы. Такие проблемы возникают практически во всех разделах математики. В математической логике для каждой теории формулируется проблема решения множества всех истинных или доводочные утверждений этой теории относительно множества всех ее предложений (теории подразделяются на разрешимые и неразрешимые в зависимости от разрешимости или неразрешимости указанной проблемы); в 1936 А. Черч установил неразрешимость проблемы разрешимости для множества всех истинных предложений логики предикатов, дальнейшие важные результаты в этом направлении принадлежат А.Тарском, А. И. Мальцеву и др.. Неразрешимые алгоритмические проблемы встречаются в алгебре (проблема тождества для полугрупп и, в частности, для групп ; первые примеры полугрупп с неразрешимой проблемой тождества были изобретены в 1947 г. независимо А. А. Марковым и Э. Постом, а пример группы с неразрешимой проблемой тождества - в 1952 г. П. С. Новиковым ); в топологии (проблема гомеоморфии, неразрешимость которой для важного класса случаев была доказана в 1958 г. А. А. Марковым ); в теории чисел (проблема решения 'язности диофантовых уравнений, неразрешимость которого была установлена в 1970 г. Ю. В. Матиясевичем ) и в др.. разделам математики.
Теория алгоритмов тесно связана:
1) с математической логикой, поскольку в терминах алгоритмов может быть изложено одно из центральных понятий математической логики - понятие исчисления (и поэтому, напр., Геделя теорема о неполноте формальных систем может быть получена как следствие теорем А. т.)
2) с основами математики, в которых одно из центральных мест занимает проблема соотношения конструктивного и неконструктивного (в частности, А. т. дает аппарат, необходимый для разработки конструктивного направления в математике); в 1965 г. А. Н. Колмогоров предложил использовать А. т. для обоснования теории информации,
3) с кибернетикой, в которой важное место занимает изучение алгоритмов управления. А. т. образует теоретический фундамент для ряда вопросов вычислительной математики.