Лямбда-исчисления - формальная система, которая используется в теоретической кибернетике для исследования определения функции, применение функции, и рекурсии. Это исчисление было предложено Алонсо Черчем и Стивеном Клини в 1930-е годы, как часть большего попытки разработать базис математики на основе функций, а не множеств (во избежание таких препятствий, как Парадокс Рассела ). Однако, Парадокс Клини-Россера демонстрирует, что лямбда исчисление не способно избежать теоретико-множественных парадоксов. Несмотря на это, лямбда исчисление оказалось удобным инструментом в исследовании вычислимости функций, и легло в основу парадигмы функционального программирования.
Лямбда исчисление может рассматриваться как идеализированная, минималистича язык, в этом смысле лямбда исчисления вроде машины Тьюринга, другой минималистической абстракции, способной определять любой алгоритм. Отличие между ними состоит в том, что лямбда исчисления соответствует функциональной парадигме определения алгоритмов, а машина Тьюринга, зато - императивной. То есть, машина Тьюринга имеет определенный «состояние» - перечень символов, которые могут варьироваться с каждой следующей инструкцией. В отличие от этого, лямбда исчисление избегает состояний, оно имеет дело с функциями, которые получают значения параметров и возвращают результаты вычислений (возможно, другие функции), но не вызывают к изменению входных данных ( постоянство ).
Ядро Лямбда-исчисления основывается не более чем на определенные переменных, области видимости переменных и упорядоченном замещении переменных выражениями. лямбда-исчисление является замкнутой языке, то есть, семантика языка может быть определена на основе эквивалентности выражений (или термов) самого языка.
Запись лямбда-выражений
Они не такие сложные, как кажутся на первый взгляд. Просто надо немного привыкнуть к префиксные формы записи. Больше нет ни инфиксних (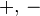 
), ни постфиксные ( x 2 ) операций. Кроме того, аргументы функций просто записываются в список после функции, разделенные пробелом. Поэтому, везде где математики пишут sin ( x ) в лямбда-исчислении пишут Sin X (хотя математики сами часто грешат опусканием скобок. Программисты в этом плане культурны). Так же вместо 
пишут 
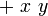, а вместо x 2 -
.
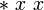Хотя скобки таки не пропадают. Они используются для группировки. Например математическое выражение sin ( x ) + 4 в лямбда-исчислении записывается как 
.
Если выражение содержит переменную, то он может описывать функцию, как зависимость своего значения от значения переменной, например f ( x ) = 3 x . Лямбда-исчисление имеет специальный синтаксис, который не обязывает задавать имя функции (как для f ). Для записи функции переводим выражение в правой части в префиксные форму (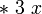 
), и дописываем впереди " ? X . ". Получаем 
. Греческая буква Лямбда имеет роль подобную той что имеет слово "function" в некоторых языках программирования. Она указывает читателю что переменная после нее - не часть выражения, а формальный параметр функции задаваемый. Точка после параметра обозначает начало тела функции.
| Язык |
Пример |
| Лямбда-исчисление |
 |
| Pascal |
Function F ( x : integer ) : Integer Begin F : = 3 * X End ;
(Не совсем лямбда-выражение, но суть та же) |
| Lisp |
( lambda ( x ) ( * 3 x ) )
|
| Python |
|
Чтобы применить созданную функцию к каким аргументам, его просто подставляют в выражение, например так: 
. Скобки вокруг функции нужны, чтобы четко знать, где она заканчивается. Если бы мы написали 
, то это могло бы восприниматься, как функция возвращающая 3 * x * 4 = = 12 x , если * - тернарных оператор, или как синтаксическая ошибка, если * - всегда бинарное.
Для удобства, мы можем обозначить нашу функцию некой буквой:
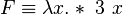
и потом просто писать F 4 .
Осталось рассмотреть еще один интересный случай:
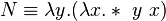
если передать 
, то она вернет нашу старую функцию . Т.е. N 3 работает как F , которой мы можем передать например 4, записав это как 
. Или, мы можем рассматривать ее как функцию от двух аргументов.
Можно записать это в сокращенной форме, без скобок:
Или еще короче:
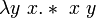
Следующий раздел этой статьи объясняет то же самое, но немного в другом стиле.
