Задачи линейного программирования

Линейное программирование — это математическая дисциплина, изучающая теорию и методы решения экстремальных задач на множествах n-мерного пространства векторов, которые задаются нераверствами и (СЛУ) системами линейных уравнений.

То есть мы видим, что слово "программирование" совсем не связано с понятием программирования. Как мы приняли считать, однако именно так называется данная дисциплина.

Леонид Витальевич Канторович в 1939 г. написал работу, которая называется «Математические методы организации и планирования производства», в ней он описал класс экстремальных задач с ограничениями, и в этой же работе он исследовал и создал эффективный метод их решения. Именно в этой работе были заложены основы линейного программирования.

Частным случаем выпуклого программирования, а также случаем математического программирования является линейное программирование. Одновременно линейное программирование — является базисом нескольких методов решения задач целочисленного и нелинейного программирования, а тажке дробно-линейного программирования.

В задаче линейного программирования возможно также интерпретировать свойства многогранников и таким образом геометрически формулировать и доказывать их.

Термин, использующийся словом «программирование» необходимо влаживать смысл «планирования». Джорджем Данцигом предложил этот термин в 1940-х гг., он одним из основоположников линейного программирования. К удивлению, но ещё до того, как компьютеры использовались для линейных задач оптимизации.

Математическая формулировка

В математической формулировне необходимо получить максимум линейной целевой функции:

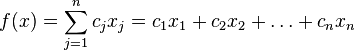
$f(x)=\sum_{j=1}^n c_jx_j=c_1x_1+c_2x_2+\ldots+c_nx_n$

Условие:

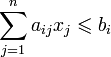$\sum_{j=1}^n a_{ij}x_j\leqslant b_i$ при $i=1,\;2,\;\ldots,\;m$ .

На xi иногда тоже накладывается набор области определия, ограничивающий в виде равенств. От этого избавиться можно, если мы будем последовательно выражать одну переменную через другие переменные, а замет подставлять её во другие равенства и неравенства и следовательно в функции f.

В линейном программировании подобную задачу называют «основной» или «стандартной».

Примеры задач линейного программирования

Максимальное паросочетание

Здесь мы рассмотрим простую задачу о максимальном паросочетании в двудольном графе.

Задача: есть несколько юношей и девушек, в задаче известно, что юноши и девушки симпатичны друг другу. Необходимо: поженить как можно больше число пар со взаимной симпатией.

Для решения поставленной задачи введём по началу переменные xij, которые соответствуют паре: i - юноши и j девушки и удовлетворяют ограничениям:

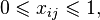
$0\leqslant x_{ij}\leqslant 1,$

$x_{1i}+x_{2i}+\ldots+x_{ni}\leqslant 1,$

$x_{i1}+x_{i2}+\ldots+x_{im}\leqslant 1,$

с целевой функцией 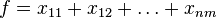$f=x_{11}+x_{12}+\ldots+x_{nm}$ . Видно, что среди оптимальных решений данной задачи линейного программирования мы найдем целочисленное значение. Переменные, равные 1 - это пара, которую нужно поженить.

Максимальный поток

Допустим мы имеем граф (с ориентированными рёбрами), в графе указана его пропускная способность для каждого ребра. В задании заданы две вершины: сток и исток. Нам нужно для каждого ребра указать, сколько через него протекать будет количество жидкости, так, чтобы максимизировать суммарный поток из истока в сток (но не больше чем его пропускная способность и жидкость не может добавляться или уходить во всех вершинах, кроме стока и истока).

Переменную xi обознчим как количество жидкости, которая протекает через i-тое ребро. Тогда:

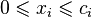$0\leqslant x_i\leqslant c_i$ ,

где ci — пропускная способность i-того ребра.

Для каждой вершины такие неравенства надо дополнить равенством количества втекающей и вытекающей жидкости, кроме стока и истока. Функция f - это разность между количеством вытекающей и втекающей жидкости в истоке.

Задача должна решить следующее задание — максимальный поток минимальной стоимости. Нам даны стоимости для каждого ребра и необходимо выбрать поток с минимальной стоимостью среди максимальных потоков. Задача сводится к двум задачам линейного программирования:

1) Нам нужно сначала решить задачу о максимальном потоке, а затем добавить к задаче ограничение 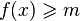$f(x)\geqslant m$ , где m — величина максимального потока, и решить задачу с новой функцией f(x) — стоимостью потока.

Задачи такого типа можна решить быстрее, чем общими алгоритмами задач линейного программирования. Это достигается за счёт особой структуры уравнений и неравенств.

Транспортная задача

Дано: Однородный груз. Нужно его перевести с n складов на m заводов. Для каждого склада i известно, сколько в нём находится груза ai, а для каждого завода известна его потребность bj в грузе. Стоимость пропорциональна перевозки и расстоянию от склада до завода (все расстояния cij от i-го склада до j-го завода известны). Решение данной задачи линейного программирования - это нахождение наиболее дешёвого плану перевозки.

xij обозначим количествов груза, перевезённого из i-го склада на j-й завод. Они удовлетворяют ограничениям:

$x_{i1}+x_{i2}+\ldots+x_{im}\leqslant a_i,$

$x_{1j}+x_{2j}+\ldots+x_{nj}\geqslant b_j.$

Функция целевая имеет вид: $f(x)=x_{11}c_{11}+x_{12}c_{12}+\ldots+x_{nm}c_{nm}$ , ее надо минимизировать.

Игра с нулевой суммой

Имеется матрица A размера $n\times m$ . Первый игрок выбирает число от 1 до n, второй — от 1 до m. Затем игроки сверяют числа и первый игрок получает aij очков, а второй ( -aij) очков (i — число, выбранное первым игроком, j — вторым). Решение данной задачи сводится к оптимальной стратегию первого игрока.

Пусть в оптимальной стратегии, например, первого игрока число i нужно выбирать с вероятностью pi. Тогда оптимальная стратегия является решением следующей задачи:

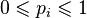$0\leqslant p_i\leqslant 1$ ,

$p_1+\ldots+p_n=1$ ,

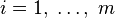$a_{1i}p_1+a_{2i}p_2+\ldots+a_{ni}p_n\geqslant c$ ( $i=1,\;\ldots,\;m$ ),

В данной задаче нам надо максимизировать функцию 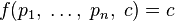$f(p_1,\;\ldots,\;p_n,\;c)=c$ . Значение c будет математическим ожиданием (в оптимальном решении) выигрыша первого игрока в наихудшем случае.

Алгоритмы решения

Симплекс-метод для решения задач линейного программирования считается наиболее известным и широко применяемым на практике. Симплекс-метод является достаточно эффективным алгоритмом. Он показывает хорошие результаты при решении прикладных задач в области линейного программирования, он является алгоритмом сэкспоненциальной сложностью.

Симплекс-метода, последовательно перебирает вершины многогранника допустимых решений при поиске оптимального решения.

В 1979 году математиком Л. Хачияном был предложен метод эллипсоидов, который разрешил проблему, остававшуюся нерешённой долгое время. Этот метод имеет совершенно другую, некомбинаторную, природу, в отличии симплекс-метода. Недостаток данного метода в том, что в вычислительном плане он оказывается неперспективным. Факт полиномиальной сложности задач способствовал к внедрению целого класса эффективных алгоритмов линейного программирования. Один из методов - это метод внутренней точки, предложенный в 1984 году Н. Кармаркаром, . Алгоритмы метода внутреней точки используют непрерывную трактовку задачи линейного программирования. В отличии от симплекс-метода, метод внутренних точек обходит точки из внутренней части области допустимых значений и использует методы логарифмических барьерных функций нелинейного программирования, которые были разработаны в 1960-х гг. Фиако (Fiacco) и МакКормиком (McCormick).

История

Леонид Витальевич Канторович в 1939 году написал и опубликовал работу под названием «Математические методы организации и планирования производства», в ней он сформулировал новый класс экстремальных задач с ограничениями, а также разработал оптимальный и эффективный метод решения. Именно здесь были были заложены начатки линейного программирования.

В первый раз метод внутренних точек имеет упоменание в 1967 году И. И. Дикиным.

Отцом линейного программирования на западе признано считать Джорджа Данцига. Он разработал симплекс-метод.