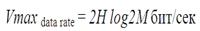
где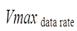 
– максимальная скорость передачи H - ширина полосы пропускания канала, выраженная в Гц, М - количество уровней сигнала, которые используются при передаче. Например, из этой формулы видно, что канал с полосой 3 кГц не может передавать двухуровневые сигналы быстрее 6000 бит/сек.
Эта теорема также показывает, что, например, бессмысленно сканировать линию чаще, чем удвоена ширина полосы пропускания. Действительно, все частоты выше этой отсутствуют в сигнале, а потому вся информация, необходимая для возобновления сигнала будет собрана при таком сканировании.
Однако, теорема Котельникова Найквиста не учитывает шум в канале, который измеряется как отношение мощности полезного сигнала к мощности шума: S/N. Эта величина измеряется в децибелах: 10log10(S/N) dB. Например, если отношение S/N равняется 10, то говорят о шуме в 10 dB если отношение равняется 100, то - 20 dB.
На случай канала с шумом есть теорема Шеннона, по которой максимальная скорость передачи данных по каналу с шумом равняется:
H log2 (1+S/N) бит/сек,
где S/N - соотношение сигнал-шум в канале.
Здесь уже не важно количество уровней в сигнале. Эта формула устанавливает теоретический предел, который редко достигается на практике. Например, по каналу с полосой пропускания в 3000 Гц и уровнем шума 30 dB (это характеристики телефонной линии) нельзя передать данные быстрее, чем со скоростью 30 000 бит/сек.
