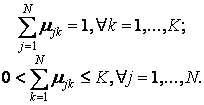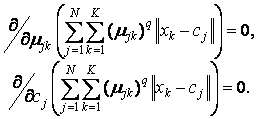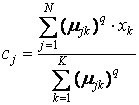Алгоритмы кластеризации | Нечеткая кластеризация

FCM-алгоритм кластеризации

Алгоритм нечеткой кластеризации называют FCM-алгоритмом (Fuzzy Classifier Means, Fuzzy C-Means). Целью FCM-алгоритма кластеризации является автоматическая классификация множества объектов, которые задаются векторами признаков в пространстве признаков. Другими словами, такой алгоритм определяет кластеры и соответственно классифицирует объекты. Кластеры представляются нечеткими множествами, и, кроме того, границы между кластерами также являются нечеткими.
FCM-алгоритм кластеризации предполагает, что объекты принадлежат всем кластерам с определенной ФП. Степень принадлежности определяется расстоянием от объекта до соответствующих кластерных центров. Данный алгоритм итерационно вычисляет центры кластеров и новые степени принадлежности объектов.

Для заданного множества К входных векторов х_k и N выделяемых кластеров с_j предполагается, что любой хк принадлежит любому с_j с принадлежностью µ_jk интервалу [0,1], где j – номер кластера, а k – номер входного вектора.

Принимаются во внимание следующие условия нормирования для µ_jk:

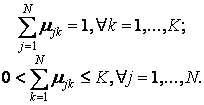
Цель алгоритма – минимизация суммы всех взвешенных расстояний :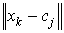

,

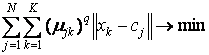где q – фиксированный параметр, задаваемый перед итерациями.

Для достижения вышеуказанной цели необходимо решить следующую систему уравнений:

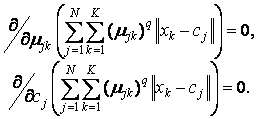
Совместно с условиями нормирования µ_jk данная система дифференциальных уравнений имеет следующее решение:

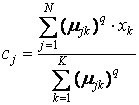
(взвешенный центр гравитации) и

Алгоритм нечеткой кластеризации выполняется по шагам

Шаг 1. Инициализация.

Выбираются следующие параметры:

• необходимое количество кластеров N, 2 < N < К;
• мера расстояний, как Евклидово расстояние;
• фиксированный параметр q (обычно 1,5);
• начальная (на нулевой итерации) матрица принадлежности 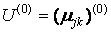 объектов х_k с учетом заданных начальных центров кластеров с_j.

Шаг 2. Регулирование позиций 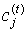центров кластеров.

На t-м итерационном шаге при известной матрице 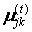 вычисляется 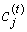в соответствии с вышеприведенным решением системы дифференциальных уравнений.

Шаг 3. Корректировка значений принадлежности µ_jk.
Учитывая известные 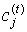, вычисляются 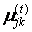, если 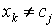, в противном случае:

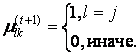
Шаг 4. Остановка алгоритма.

Алгоритм нечеткой кластеризации останавливается при выполнении следующего условия:

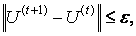
где    ||   || – матричная норма (например, Евклидова норма);
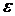 – заранее задаваемый уровень точности.

Решение задач кластеризации

Существуют два способа решения задач кластеризации в Matlab: с использованием командной строки или графического интерфейса пользователя. Рассмотрим первый из указанных способов.

Для нахождения центров кластеров в Matlab имеется, встроенная функция fcm, описание которой представлено ниже.
Описание функции:

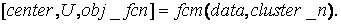
Аргументами данной функции являются:

1) data – множество данных, подлежащих кластеризации, каждая строка описывает точку в многомерном пространстве характеристик;
2) cluster_n — количество кластеров (более одного).

Функцией возвращаются следующие параметры:

1) center – матрица центров кластеров, каждая строка которой содержит координаты центра отдельного кластера;
2) U – результирующая матрица ФП;
3) obj_fcn – значение целевой функции на каждой итерации.

Пример П11. Программа нечеткой кластеризации.

// загрузка данных, подлежащих кластеризации, из файла
load fcmdata.dat;
// определение центра кластеризации (два кластера)
[center, U, obj_fcm] = fcm( fсmdata, 2);
// определение максимальной степени принадлежности
// отдельного элемента данных кластеру
maxU = max(U);
// распределение строк матрицы данных между соответствующими
// кластерами
index1 = find (U(1, :) == maxU);
index2 = find(U(2, :) = maxU);
// построение данных, соответствующих первому кластеру
plot (fcmdata (index1, 1), fcmdata (index1, 2),' ko', 'markersize', 5, 'LineWidth' ,1);
hold on
// построение данных, соответствующих второму кластеру
plot(fcmdata (index2, 1), fcmdata(index2, 2), 'kx', 'markersize', 5, 'LineWidth', 1);
// построение кластерных центров
plot(center(1, 1), center(1, 2), 'ko', 'markersize', 15,  'LineWidth', 2)
plot (center (2, 1), center (2, 2),  'kx', 'markersize', 15, 'LineWidth', 2)

На рис. П15 представлено множество данных, подлежащих кластеризации и найденные центры кластеров для примера П.11.

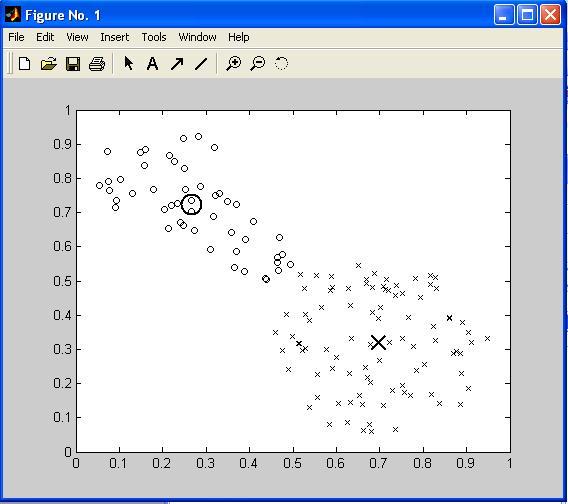
Рис. П15. Множество анализируемых данных и центры кластеров

Функция fcm выполняется итерационно до тех пор, пока изменения целевой функции превышают некоторый заданный порог. На каждом шаге в командном окне Маtlab выводятся порядковый номер итерации и соответствующее текущее значение целевой функции.

Для оценки динамики изменения значений целевой функции используется команда построения графика plot(obj_fcm). Результаты примера П11 показаны на рис. П16.

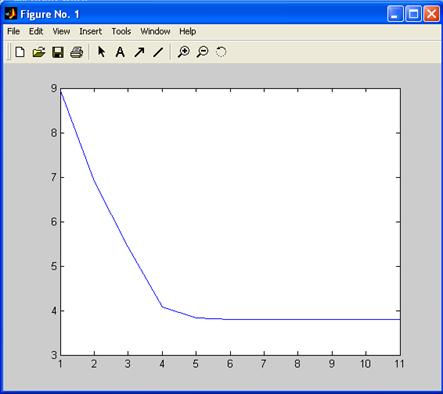
Рис. П16. График изменения значений целевой функции

Функцию кластеризации можно вызвать с дополнительным набором параметров: fcm (data, cluster_n, options). Дополнительные аргументы используются для управления процессом кластеризации:

• options(1) – показатель степени для матрицы U (по умолчанию – 2.0);
• options(2) – максимальное количество итераций (по умолчанию – 100);
• options(3) – предельное изменение значений целевой функции (по умолчанию – 1е-5);
• options(4) – отображение информации на каждом шаге (по умолчанию – 1).

Пример определения функции fcm с дополнительными параметрами:

[center, U, obj_fcn] = fсm(fcmdata, 2, [2,100,le-5,1]).

Второй способ решения задач кластеризации в Matlab основан на использовании ГИП, который вызывается командой findcluster. Главное окно инструмента кластеризации показано на рис. П17.

Кнопка <Load Data> используется для загрузки подлежащих кластеризации исходных данных следующего формата: каждая строка представляет собой точку в многомерном пространстве характеристик, количество строк соответствует количеству точек (элементов данных). Графическую интерпретацию исходных данных можно наблюдать в одноименном окне главного окна инструмента.

Выбор типа алгоритма кластеризации осуществляется с ис­пользованием ниспадающего меню Methods (пункт меню – fcm). Далее определяются параметры алгоритма кластеризации:

• количество кластеров (строка ввода – Cluster Num);
• максимальное количество итераций (строка ввода — Мах Iteration#);
• минимальное значение улучшения целевой функции (строка ввода — Min. Improvement);
• показатель степени при матрице ФП (строка ввода — Exponent).

После определения необходимых значений указанных параметров осуществляется запуск алгоритма кластеризации с помощью кнопки <Start>. Количество произведенных итераций и значение целевой функции можно просмотреть в нижней части главного окна инструмента кластеризации.

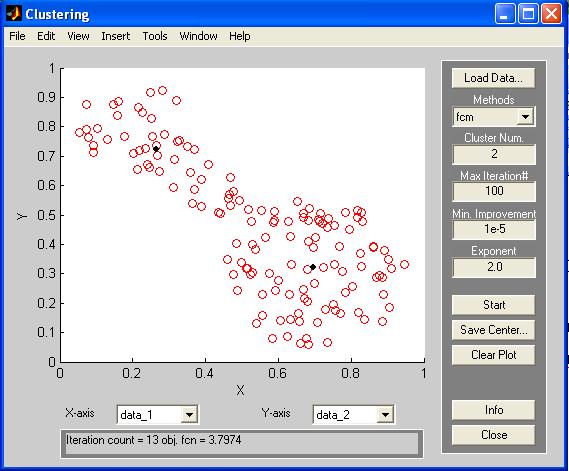
Рис. П17. Главное окно кластеризации в Matlab

Координаты найденных центров кластеров можно сохранить, щелкнув мышью по кнопке <Save Center...>. Каждая строка матрицы в файле представляет собой набор координат отдельного кластера. Количество строк соответствует количеству кластеров.