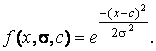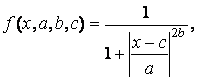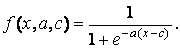Функции принадлежности
Инструментарий нечеткой логики (ИНЛ) в составе пакета Matlab содержит 11 встроенных типов функций принадлежности (ФП), формируемых на основе кусочно-линейных функций, распределения Гаусса, сигмоидной кривой, квадратических и кубических полиномиальных кривых. К наиболее простым ФП можно отнести треугольную и трапециевидную. Наименование треугольной ФП – trimf (triangle membership function). В параметрическом виде она представляет собой не что иное, как набор трех точек, образующих треугольник.
Описание функции:у = trimf(x, [abс]),
где вектор х – базовое множество, на котором определяется ФП. Величины а и с задают основание треугольника, b– его вершину.
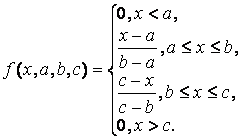
В аналитическом виде треугольная ФП может быть задана следующим образом (рис. П1, а):
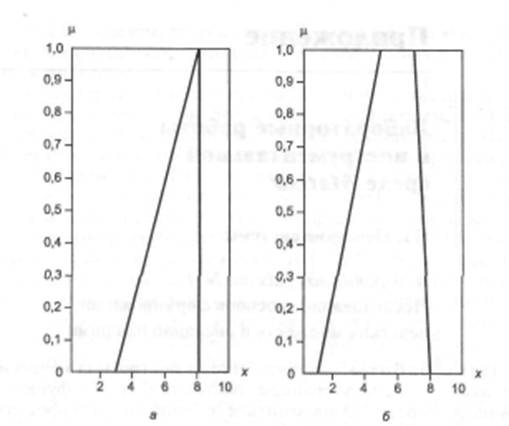
Рис. П1. Треугольная (а) и трапециевидная (б) функции принадлежности
Далее рассмотрим примеры использования различных ФП в системе.
Примеры представляют собой фрагменты программ и комментариев на языке пакета Matlab.
Пример П1. Программа использования ФП trimf
х = 0 : 0,1 : 10; Задается базовое множество
у = trimf(x, [3 6 8]); Определяется треугольная ФП
plot (х, у) ; Выводится график функции
xlabel('trimf(x, P), P = [3 6 8]'); Подписывается график под осью абсцисс
Трапециевидная ФП - trapmf (trapezoid membership function) – отличается от предыдущей функции лишь тем, что имеет верхнее основание.
Описание функции: у = trapmf(х, [abс d]),
где параметры а и d – нижнее основание трапеции;
b и с –верхнее основание трапеции (рис. П1, б).
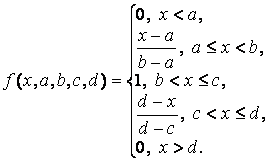
Аналитическая запись трапециевидной функции имеет вид:
Одно из основных достоинств треугольных и трапециевидных ФП – их простота. На основе функции распределения Гаусса можно построить ФП двух видов: простую функцию принадлежности Гаусса и двухстороннюю, образованную с помощью различных функций распределения Гаусса. Первая из них обозначается gaussmf, а вторая – gauss2mf.
Описание функции:
у = gaussmf(x, [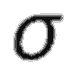 , с]).
, с]).
Симметричная функция Гаусса зависит от двух параметров 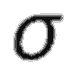 и с (рис. П.2, а):
и с (рис. П.2, а):
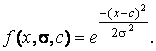
Пример П2. Программа использования ФП gaussmf
X= 0 : 0,1 : 10;
Y= gaussmf(х, [2 5]);
plot (х, у);
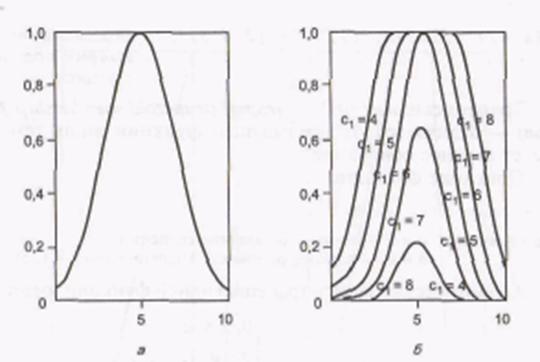
Рис. П2. Простая (а) и двухсторонняя (б) функции принадлежности Гаусса.
Описание функции: у = gauss2mf (x, [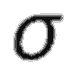 1, с1,
1, с1, 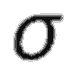 2, c2]).
2, c2]).
Последнее выражение является комбинацией двух различных функций распределения Гаусса. Первая определяется параметрами 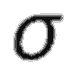 1 и с1 и задает форму левой стороны, а вторая (параметры
1 и с1 и задает форму левой стороны, а вторая (параметры 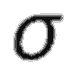 2, c2) – правой стороны ФП.
2, c2) – правой стороны ФП.
Если с1 < c2, то в этом случае функция gauss2mf достигает своего максимального значения на уровне 1. Иначе – максимальное значение функции меньше 1 (рис. П2, б).
Пример ПЗ. Программа использования ФП gauss2mf
х = (0 : 0,1 : 10)';
y1 = gauss2mf(x, [2 4 1 8]);
у2 = gauss2mf(x, [2 5 1 7]);
уЗ = gauss2mf(x, [2 6 1 6]);
у4 = gauss2mf(x, [2 7 1 5]);
У5 = gauss2mf(x, [2 8 1 4]);
Plot (x, [y1 у2 уЗ у4 у5]);
Символ «'» в строке определения базового множества х показывает транспонированность базового множества.
Следующей функцией, которая позволяет представлять нечеткие субъективные предпочтения, является ФП «обобщенный колокол» и обозначается gbellmf(generalized bell shape membership function).
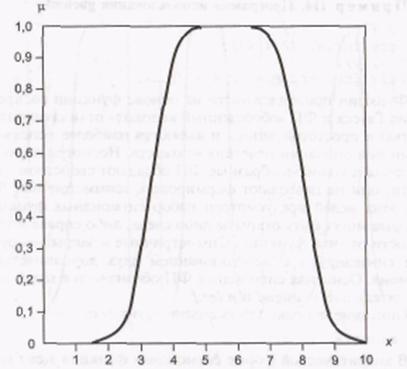
gbellmf, P = [2 4 6]
Рис. П3. Функция принадлежности «обобщенный колокол»
Ее отличие от рассмотренных ранее ФП заключается в добавлении третьего параметра, что позволяет осуществлять плавный переход между нечеткими множествами.
Описание функции: у = gbellmf (x, [а b с]) .
Функция «обобщенный колокол» зависит от трех параметров и имеет следующую аналитическую запись:
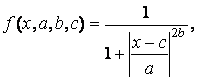
где с – определяет расположение центра ФП; а и b – оказывают влияние на форму кривой (рис. ПЗ).
Пример П4. Программа использования gbellmf
х = 0 : 0,1 : 10;
у = gbellmf (х, [2 4 6]);
plot(x, у);
xlabel('gbellmf, р = [2 4 61]').
Функции принадлежности на основе функции распределения Гаусса и ФП “обобщенный колокол” отличаются гладкостью и простотой записи и являются наиболее используемыми при описании нечетких множеств. Несмотря на то, что гауссовы и колоколообразные ФП обладают свойством гладкости, они не позволяют формировать асимметричные ФП. Для этих целей предусмотрен набор сигмоидных функций, которые могут быть открыты либо слева, либо справа в зависимости от типа функции. Симметричные и закрытые функции синтезируют с использованием двух дополнительных сигмоид. Основная сигмоидная ФП обозначается sigmf, а дополнительные – dsigmf и psigmf.
Описание основной сигмоидной функции: у = sigmf (х, [a с]).
В аналитической форме сигмоидная функция sigmf записывается следующим образом:
В зависимости от знака параметра a рассматриваемая ФП будет открыта или справа или слева (рис. П4, а), что позволит применять ее при описании таких нечетких понятий, как «очень большой», «крайне отрицательно» и др.
Описание дополнительной сигмоидной функции: у = dsigmf(x, (a1, c1, а2, с2)) .
ФП dsigmf зависит от четырех параметров a1, c1, а2 и с2 и определяется как разность двух сигмоидных функций: f(х, a1, c1) - f(x, а2, с2) (рис. П4, б).
Описание дополнительной сигмоидной функции: у = psigmf (x, [a1, c1, а2, с2]) .
ФП psigmf, так же как и предыдущая функция, зависит от четырех параметров a1, c1, а2, с2 и определяется как произведение двух сигмоидных функций f(х, a1, c1)*f(x, а2, с2) (рис. П4, в).
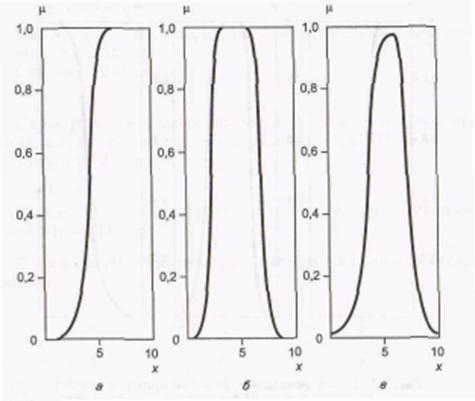
Рис. П4. Сигмоилные функции принадлежности:
а – основная односторонняя; б – дополнительная двухсторонняя;
в — дополнительная несимметричная
Пример П5. Программа использования сигмоидных функций
х = 0 : 0,1 : 10; определяется базовое множество
subplot (1, 3, 1); формируется матрица графиков (3x1)
первый элемент – текущий
y=sigmf(x,[2 4]);
plot (х, у); выводится график в первый элемент матрицы
xlabel ('sigmf, P = [2 4]')
subplot (1, 3, 2); выбирается второй текущий элемент
у = dsigmf (x, [5 2 5 7]);
plot (х, у); выводится график во второй элемент матрицы
xlabel ('dsigmf, Р = [5 2 5 7]')
subplot (1, 3, 3); выбирается третий текущий элемент
у = psigmf (x, [2 3 -5 8]);
plot (х, у); выводится график в третий элемент матрицы
xlabel ('psigmf, P= [2 3 -5 8]');
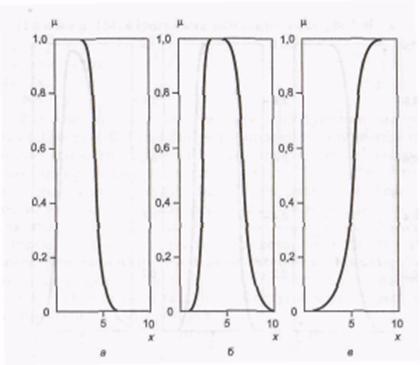
Рис. П5. Полиномиальные функции принадлежности:
а – Z-функция; б – PI-функикя; в – S-функиия
Инструментарий нечеткой логики (fuzzy logic toolbox) в составе Matlabпредоставляет возможность формирования ФП на основе полиномиальных кривых. Соответствующие функции называются Z-функции (zmf), РI-функции (pimf) и S-функции (smf). Функция zmfпредставляет собой асимметричную полиномиальную кривую, открытую слева (рис. П5, а), функция smf – зеркальное отображение функции zmf (рис. П5, в). Соответственно функция pimf равна нулю в правом и левом пределах и принимает значение, равное единице, в середине некоторого отрезка (рис. П5, б).
Описание функции: у = zmf(x, [ab]).
Параметры а и b определяют экстремальные значения кривой (рис. П5, а).
Описание функции: у = pimf (x, [ab с d]).
Параметры а и dзадают переход функции в нулевое значение, а параметры bи с – в единичное (рис. П5, б).
Описание функции: у = smf (х, [а b]) .
Параметры а и bопределяют экстремальные значения кривой (рис. П5, в).
Пример П6. Программа использования полиномиальных кривых
х = 0 : 0,1 : 10;
subplot(1, 3, 1);
у = zmf(x, (3 7]);
plot (х, у);
xlabel (' zmf, P = [3 7]');
subplot (1, 3, 2);
у = pimf(x, [1 4 5 10]);
plot (x, у);
xlabel ('pimf, P = [1 4 5 10]');
subplot (1, 3, 3);
у = smf (x, [1 8]);
plot(x, y);
xlabel ('smf, P=[1 8]').
Помимо рассмотренных выше функций, позволяющих представлять нечеткие множества, в Mattabимеется возможность формировать собственные ФП или модифицировать встроенные.