Построение графиков функции одной переменной в MatLab

1. Графики функций в линейном масштабе

MatLab обладает хорошо развитыми графическими возможностями для визуализации данных. Рассмотрим в начале построение простейшего графика функции одной переменной на примере функции

,

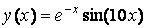определенной на отрезке [0, 1]. Вывод функции в виде графика состоит из следующих этапов:

1. Задание вектора значений аргумента х.
2. Вычисление вектора у значений функции y(х).
3. Вызов команды  plot  для построения графика.

Команды для задания вектора х и вычисления функции лучше завершать точкой с запятой для подавления вывода в командное окно их значений (после команды plot точку с запятой ставить необязательно, т. к. она ничего не выводит в командное окно).

» х = [0:0.05:1];
» у = ехр(-х).*sin(10*x);
» plot(x, у)

После выполнения команд на экране появляется окно Figure No. 1 с графиком функции. Окно содержит меню, панель инструментов и область графика. В дальнейшем будут описаны команды, специально предназначенные для оформления графика. Сейчас нас интересует сам принцип построения графиков и некоторые простейшие возможности визуализации функций.

Для построения графика функции в рабочей среде MatLab должны быть определены два вектора одинаковой размерности, например х и у. Соответствующий массив х содержит значения аргументов, а у — значения функции от этих аргументов. Команда plot соединяет точки с координатами (x(i), y(i)) прямыми линиями, автоматически масштабируя оси для оптимального расположения графика в окне. При построении графиков удобно расположить на экране основное окно MatLab и окно с графиком рядом так, чтобы они не перекрывались.

Построенный график функции имеет изломы. Для более точного построения графика функцию необходимо вычислить y(х) в большем числе точек на отрезке [0, 1], т.е. задать меньший шаг при вводе вектора х:

» х = [0:0.01:1];
» у = ехр(-х).*sin(10*x);
» plot(x, у)

В результате получается график функции в виде более плавной кривой.
Сравнение нескольких функций удобно производить, отобразив их графики на одних осях. Например, построим на отрезке [-1, -0.3] графики функций

,

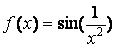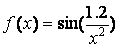
при помощи следующей последовательности команд:

» х = [-1:0.005:-0.3];
» f = sin(x.^-2);
» g = sin(1.2*x.^-2);
» plot(x, f, x, g)

Функции необязательно должны быть определены на одном и том же отрезке. В этом случае при построении графиков MatLab выбирает максимальный отрезок, содержащий остальные. Важно только в каждой паре векторов абсцисс и ординат указать соответствующие друг другу вектора, например:

» х1 = [-1:0.005:-0.3];
» f = sin(x1.^-2);
» х2 = [-1:0.005:0.3];
» g = sin(1.2*x2.^-2);
» plot(x1, f, x2, g)

Аналогичным образом при помощи задания в plot через запятую пар аргументов вида: вектор абсцисс, вектор ординат, осуществляется построение графиков произвольного числа функций.

Замечание 1
Использование plot с одним аргументом - вектором - приводит к построению "графика вектора", т.е. зависимости значений элементов вектора от их номеров. Аргументом plot может быть и матрица, в этом случае на одни координатные оси выводятся графики столбцов.
Иногда требуется сравнить поведение двух функций, значения которых сильно отличаются друг от друга. График функции с небольшими значениями практически сливается с осью абсцисс, и установить его вид не удается. В этой ситуации помогает функция plotyy, которая выводит графики в окно с двумя вертикальными осями, имеющими подходящий масштаб.
Сравните, например, две функци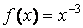и:   и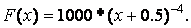 

» х = [0.5:0.01:3];
» f = х.^-3;
» F = 1000*(х+0.5).^-4;
» plotyy(x, f, x, F)

При выполнении этого примера обратите внимание, что цвет графика совпадает с цветом соответствующей ему оси ординат.
Функция plot использует линейный масштаб по обеим координатным осям. Однако MatLab предоставляет пользователю возможность строить графики функций одной переменной в логарифмическом или полулогарифмическом масштабе.

2. Графики функций в логарифмических масштабах

Для построения графиков в логарифмическом и полулогарифмическом масштабах служат следующие функции:
- loglog (логарифмический масштаб по обеим осям);
- semilogx (логарифмический масштаб только по оси абсцисс);
-semilogy (логарифмический масштаб только по оси ординат).
Аргументы loglog, semilogx и semilogy задаются в виде пары векторов значений абсцисс и ординат так же, как для функции plot, описанной в предыдущем пункте. Построим, например, графики функци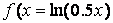й   и 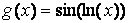   на отрезке [0.1, 5] в логарифмическом масштабе по оси х:

» х = [0.1:0.01:10];
» f = log(0.5*x);
» g = sin(log(x));
» semilogx(x, f, x ,g)

3. Задание свойств линий на графиках функций

Построенные графики функций должны быть максимально удобными для восприятия. Часто требуется нанести маркеры, изменить цвет линий, а при подготовке к монохромной печати — задать тип линии (сплошная, пунктирная, штрих-пунктирная и т.д.). MatLab предоставляет возможность управлять видом графиков, построенных при помощи plot, loglog, semilogx и semilogy, для чего служит дополнительный аргумент, помещаемый за каждой парой векторов. Этот аргумент заключается в апострофы и состоит из трех символов, которые определяют: цвет, тип маркера и тип линии. Используется одна, две или три позиции, в зависимости от требуемых изменений. В таблице  приведены возможные значения данного аргумента с указанием результата.

Если, например, необходимо построить первый график красными точечными маркерами без линии, а второго график - черной пунктирной линией, то следует использовать команду plot(x, f, 'r.', х, g, 'k:').

4. Оформление графиков функций

Удобство использования графиков во многом зависит от дополнительных элементов оформления: координатной сетки, подписей к осям, заголовка и легенды. Сетка наносится командой grid on, подписи к осям размещаются при помощи xlabel, ylabel, заголовок дается командой title. Наличие нескольких графиков на одних осях требует помещения легенды командой legend с информацией о линиях. Все перечисленные команды применимы к графикам как в линейном, так и в логарифмическом и полулогарифмическом масштабах. Следующие команды выводят графики изменения суточной температуры, которые снабжены всей необходимой информацией.

» time = [0 4 7 9 10 11 12 13 13.5 14 14.5 15 16 17 18 20 22];
» temp1 = [14 15 14 16 18 17 20 22 24 28 25 20 16 13 13 14 13];
» temp2 = [12 13 13 14 16 18 20 20 23 25 25 20 16 12 12 11 10];
» plot(time, temp1, 'ro-', time, temp2, 'go-')
» grid on
» title('Суточные температуры')
» xlabel('Время (час.)')
» ylabel('Температура (С)')
» legend('10 мая1,  11 мая')

При добавлении легенды следует учесть, что порядок и количество аргументов команды legend должны соответствовать линиям на графике. Последним дополнительным аргументом может быть положение легенды в, графическом окне:

• —1 - вне графика в правом верхнем углу графического окна;
• 0 — выбирается лучшее положение в пределах графика так, чтобы как можно меньше перекрывать сами графики;
• 1 — в верхнем правом углу графика (это положение используется по умолчанию);
• 2 — в верхнем левом углу графика;
• 3 — в нижнем левом углу графика;
• 4 — в нижнем правом углу графика.

В заголовке графика, легенде и подписях осей допускается добавление формул и изменение стилей шрифта при помощи формата ТеХ.
MatLab выводит графики разным цветом. Монохромный принтер напечатает графики различными оттенками серого цвета, что не всегда удобно. Команда  plot  позволяет легко задать стиль и цвет линий, например

» plot(x,f,'k-',x,g,'k:')

осуществляет построение первого графика сплошной черной линией, а второго - черной пунктирной. Аргументы 'k-' и 'k:' задают стиль и цвет первой и второй линий. Здесь k означает черный цвет, а дефис или двоеточие - сплошную или пунктирную линию. Окно с графиком можно закрыть, нажав на кнопку с крестиком в правом верхнем углу.