Урок 7 — Графики в Matlab. Построение графиков и таблиц в Матлабе

1. Построение таблиц значений функции одной переменной в пакете MatLab

Отображение функции в виде таблицы удобно, если имеется сравнительно небольшое число значений функции. Пусть требуется вывести в командное окно таблицу значений функции

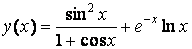
в точках 0.2, 0.3, 0.5, 0.8, 1.3, 1.7, 2.5.
Задача решается в два этапа.
1. Создается вектор-строка  х,  содержащая координаты заданных точек.
2. Вычисляются значения функции  y(х)от каждого элемента вектора х и записываются полученные значения в вектор-строку  у.
Значения функции необходимо найти для каждого из элементов вектор-строки х, поэтому операции в выражении для функции должны выполняться поэлементно.

» х = [0.2 0.3 0.5 0.8 1.3 1.7 2.5]
х =
0.2000  0.3000  0.5000  0.8000  1.3000  1.7000  2.5000 » у = sin(x).^2./(l+cos(x))+exp(-x).*log(x)
У =
-1.2978 -0.8473 -0.2980  0.2030  0.8040  1.2258  1.8764

Обратите внимание, что при попытке использования операций возведения в степень ^, деления / и умножения * (которые не относятся к поэлементным) выводится сообщение об ошибке уже при возведении sin(x) в квадрат:

» у = sin(х)^2/(1+соз(х))+exp(-x)*log(x)
??? Error using ==> ^
Matrix must be square.

Дело в том, что в MatLab операции * и ^ применяются для перемножения матриц соответствующих размеров и возведения квадратной матрицы в степень.
Таблице можно придать более удобный для чтения вид, расположив значения функции непосредственно под значениями аргумента:

» х
х =
0.2000  0.3000  0.5000  0.8000  1.3000  1.7000  2.5000 » у
у =
-1.2978 -0.8473 -0.2980  0.2030  0.8040  1.2258  1.8764

Часто требуется вывести значение функции в точках отрезка, отстоящих друг от друга на равное расстояние (шаг). Предположим, что необходимо вывести таблицу значений функции y(х)наотрезке [1, 2] с шагом 0.2. Можно, конечно, ввести вектор-строку значений аргумента х=[1, 1.2, 1.4, 1.6, 1.8, 2.0] из командной строки и вычислить все значения функции так, как описано выше. Однако, если шаг будет не 0.2, а, например 0.01, то предстоит большая работа по вводу вектора х.
В MatLab предусмотрено простое создание векторов, каждый элемент которых отличается от предшествующего на постоянную величину, т.е. на шаг. Для ввода таких векторов служит двоеточие (не путайте с индексацией при помощи двоеточия). Следующие два оператора приводят к формированию одинаковых вектор-строк. Условно можно записать

» х = [1, 1.2, 1.4, 1.6, 1.8, 2.0]
х =
1.0000   1.2000   1.4000   1.6000   1.8000   2.0000
» х = [1:0.2:2]
х =
1.0000   1.2000   1.4000   1.6000   1.8000   2.0000

Условно можно записать

х = [начальное значение : шаг : конечное значение]

Необязательно заботиться о том, чтобы сумма предпоследнего значения  шага равнялась бы конечному значению, например, при выполнении следующего оператора присваивания

» х = [1:0.2:1.9]
х =
1.0000  1.2000  1.4000  1.6000  1.8000

Вектор-строка заполнится до элемента, не превосходящего определенное нами конечное значение. Шаг может быть и отрицательным:

» х = [1.9:-0.2:1]
х =
1.9000  1.7000  1.5000  1.3000  1.1000

В случае отрицательного шага для получения непустой вектор-строки начальное значение должно быть больше конечного.
Для заполнения вектор-столбца элементами, начинающимися с нуля и заканчивающимися 0.5 с шагом 0.1, следует заполнить вектор-строку, а затем использовать операцию транспонирования:

» х = [0:0.1:0.5]'
х =
0
0.1000
0.2000
0.3000
0.4000
0.5000

Обратите внимание, что элементы вектора, заполняемого при помощи двоеточия, могут быть только вещественными, поэтому для транспонирования можно использовать апостроф вместо точки с апострофом.
Шаг, равный единице, допускается не указывать при автоматическом заполнении:

» х = [1:5]
х =
1  2  3  4  5

Пусть требуется вывести таблицу значений функции

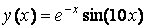
на отрезке [0, 1] с шагом 0.05,
Для выполнения этого задания необходимо произвести следующие действия:
1. Сформировать вектор-строку  х  при помощи двоеточия.
2. Вычислить значения у(х)отэлементов х.
3. Записать результат в вектор-строку  y.
4. Вывести  хи у.

» х = [0:0.05:1];
» у = ехр(-х).*sin(10*x);
» х
х =
Columns 1 through 7
О  0.0500  0.1000  0.1500  0.2000  0.2500  0.3000
Columns 8 through 14
0.3500  0.4000  0.4500  0.5000  0.5500  0.6000  0.6500
Columns 15 through 21
0.7000  0.7500  0.8000  0.8500  0.9000  0.9500  1.0000
» у
У =
Columns 1 through 7
0  0.4560  0.7614  0.8586  0.7445  0.4661  0.1045
Columns 8 through 14
-0.2472 -0.5073 -0.6233 -0.5816 -0.4071  -0.1533  0.1123
Columns 15 through 21
0.3262  0.4431  0.4445  0.3413  0.1676  -0.0291 -0.2001

Вектор-строки x и yсостоят из двадцати одного элемента, и не помещается на экране в одну строку, поэтому выводятся по частям. Так как х иy хранятся в двумерных массивах размерностью один на двадцать один, то выводятся по столбцам, каждый из которых состоит из одного элемента. Сначала выводятся столбцы с первого по седьмой (columns 1 through 7), затем - с восьмого по четырнадцатый (columns 8 through 14), и, наконец, - с пятнадцатого по двадцать первый (columns 15 through 21). Более наглядным и удобным является графическое представление функции.

2. Построение графиков функции одной переменной

2.1. Графики функций в линейном масштабе

MatLab обладает хорошо развитыми графическими возможностями для визуализации данных. Рассмотрим в начале построение простейшего графика функции одной переменной на примере функции

,

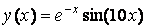определенной на отрезке [0, 1]. Вывод функции в виде графика состоит из следующих этапов:
1. Задание вектора значений аргумента х.
2. Вычисление вектора у значений функции y(х).
3. Вызов команды  plot  для построения графика.
Команды для задания вектора х и вычисления функции лучше завершать точкой с запятой для подавления вывода в командное окно их значений (после команды plot точку с запятой ставить необязательно, т. к. она ничего не выводит в командное окно).

» х = [0:0.05:1];
» у = ехр(-х).*sin(10*x);
» plot(x, у)

После выполнения команд на экране появляется окно Figure No. 1 с графиком функции. Окно содержит меню, панель инструментов и область графика. В дальнейшем будут описаны команды, специально предназначенные для оформления графика. Сейчас нас интересует сам принцип построения графиков и некоторые простейшие возможности визуализации функций.
Для построения графика функции в рабочей среде MatLab должны быть определены два вектора одинаковой размерности, например х и у. Соответствующий массив х содержит значения аргументов, а у — значения функции от этих аргументов. Команда plot соединяет точки с координатами (x(i), y(i)) прямыми линиями, автоматически масштабируя оси для оптимального расположения графика в окне. При построении графиков удобно расположить на экране основное окно MatLab и окно с графиком рядом так, чтобы они не перекрывались.
Построенный график функции имеет изломы. Для более точного построения графика функцию необходимо вычислить y(х) в большем числе точек на отрезке [0, 1], т.е. задать меньший шаг при вводе вектора х:

» х = [0:0.01:1];
» у = ехр(-х).*sin(10*x);
» plot(x, у)

В результате получается график функции в виде более плавной кривой.
Сравнение нескольких функций удобно производить, отобразив их графики на одних осях. Например, построим на отрезке [-1, -0.3] графики функций
,

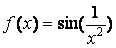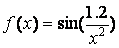
при помощи следующей последовательности команд:

» х = [-1:0.005:-0.3];
» f = sin(x.^-2);
» g = sin(1.2*x.^-2);
» plot(x, f, x, g)

Функции необязательно должны быть определены на одном и том же отрезке. В этом случае при построении графиков MatLab выбирает максимальный отрезок, содержащий остальные. Важно только в каждой паре векторов абсцисс и ординат указать соответствующие друг другу вектора, например:

» х1 = [-1:0.005:-0.3];
» f = sin(x1.^-2);
» х2 = [-1:0.005:0.3];
» g = sin(1.2*x2.^-2);
» plot(x1, f, x2, g)

Аналогичным образом при помощи задания в plot через запятую пар аргументов вида: вектор абсцисс, вектор ординат, осуществляется построение графиков произвольного числа функций.

Замечание 1

Использование plot с одним аргументом - вектором - приводит к построению "графика вектора", т.е. зависимости значений элементов вектора от их номеров. Аргументом plot может быть и матрица, в этом случае на одни координатные оси выводятся графики столбцов.
Иногда требуется сравнить поведение двух функций, значения которых сильно отличаются друг от друга. График функции с небольшими значениями практически сливается с осью абсцисс, и установить его вид не удается. В этой ситуации помогает функция plotyy, которая выводит графики в окно с двумя вертикальными осями, имеющими подходящий масштаб.
Сравните, например, две функци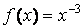и:   и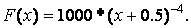 

» х = [0.5:0.01:3];
» f = х.^-3;
» F = 1000*(х+0.5).^-4;
» plotyy(x, f, x, F)

При выполнении этого примера обратите внимание, что цвет графика совпадает с цветом соответствующей ему оси ординат.
Функция plot использует линейный масштаб по обеим координатным осям. Однако MatLab предоставляет пользователю возможность строить графики функций одной переменной в логарифмическом или полулогарифмическом масштабе.

2.2. Графики функций в логарифмических масштабах

Для построения графиков в логарифмическом и полулогарифмическом масштабах служат следующие функции:
- loglog (логарифмический масштаб по обеим осям);
- semilogx (логарифмический масштаб только по оси абсцисс);
-semilogy (логарифмический масштаб только по оси ординат).

Аргументы loglog, semilogx и semilogy задаются в виде пары векторов значений абсцисс и ординат так же, как для функции plot, описанной в предыдущем пункте. Построим, например, графики функци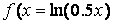й   и 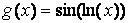   на отрезке [0.1, 5] в логарифмическом масштабе по оси х:

» х = [0.1:0.01:10];
» f = log(0.5*x);
» g = sin(log(x));
» semilogx(x, f, x ,g)

2.3. Задание свойств линий на графиках функций

Построенные графики функций должны быть максимально удобными для восприятия. Часто требуется нанести маркеры, изменить цвет линий, а при подготовке к монохромной печати — задать тип линии (сплошная, пунктирная, штрих-пунктирная и т.д.). MatLab предоставляет возможность управлять видом графиков, построенных при помощи plot, loglog, semilogx и semilogy, для чего служит дополнительный аргумент, помещаемый за каждой парой векторов. Этот аргумент заключается в апострофы и состоит из трех символов, которые определяют: цвет, тип маркера и тип линии. Используется одна, две или три позиции, в зависимости от требуемых изменений. В таблице  приведены возможные значения данного аргумента с указанием результата.

Таблица

Если, например, необходимо построить первый график красными точечными маркерами без линии, а второго график - черной пунктирной линией, то следует использовать команду plot(x, f, 'r.', х, g, 'k:').

2.4. Оформление графиков функций

Удобство использования графиков во многом зависит от дополнительных элементов оформления: координатной сетки, подписей к осям, заголовка и легенды. Сетка наносится командой grid on, подписи к осям размещаются при помощи xlabel, ylabel, заголовок дается командой title. Наличие нескольких графиков на одних осях требует помещения легенды командой legend с информацией о линиях. Все перечисленные команды применимы к графикам как в линейном, так и в логарифмическом и полулогарифмическом масштабах. Следующие команды выводят графики изменения суточной температуры, которые снабжены всей необходимой информацией.

» time = [0 4 7 9 10 11 12 13 13.5 14 14.5 15 16 17 18 20 22];
» temp1 = [14 15 14 16 18 17 20 22 24 28 25 20 16 13 13 14 13];
» temp2 = [12 13 13 14 16 18 20 20 23 25 25 20 16 12 12 11 10];
» plot(time, temp1, 'ro-', time, temp2, 'go-')
» grid on
» title('Суточные температуры')
» xlabel('Время (час.)')
» ylabel('Температура (С)')
» legend('10 мая,  11 мая')

При добавлении легенды следует учесть, что порядок и количество аргументов команды legend должны соответствовать линиям на графике. Последним дополнительным аргументом может быть положение легенды в, графическом окне:

* —1 — вне графика в правом верхнем углу графического окна;
* 0 — выбирается лучшее положение в пределах графика так, чтобы как можно меньше перекрывать сами графики;
* 1 — в верхнем правом углу графика (это положение используется по умолчанию);
* 2 — в верхнем левом углу графика;
* 3 — в нижнем левом углу графика;
* 4 — в нижнем правом углу графика.

В заголовке графика, легенде и подписях осей допускается добавление формул и изменение стилей шрифта при помощи формата ТеХ.
MatLab выводит графики разным цветом. Монохромный принтер напечатает графики различными оттенками серого цвета, что не всегда удобно. Команда  plot  позволяет легко задать стиль и цвет линий, например

» plot(x,f,'k-',x,g,'k:')

осуществляет построение первого графика сплошной черной линией, а второго - черной пунктирной. Аргументы 'k-' и 'k:' задают стиль и цвет первой и второй линий. Здесь k означает черный цвет, а дефис или двоеточие - сплошную или пунктирную линию. Окно с графиком можно закрыть, нажав на кнопку с крестиком в правом верхнем углу.

3. Построение графиков функций двух переменных

Построение графика функции двух переменных в MatLab на прямоугольной области определения переменных включает два предварительных этапа:
1. Разбиение области определения прямоугольной сеткой.
2. Вычисление значений функции в точках пересечения линий сетки и запись их в матрицу.
Построим график функции  z(x, у)= х2 + у2  на области определения в виде квадрата  х принадлежит [0, 1], y - [0, 1].  Необходимо разбить квадрат равномерной сеткой (например, с шагом 0.2) и вычислить значения функций в узлах, обозначенных точками.
Удобно использовать два двумерных массива  х и у,  размерностью шесть на шесть для хранения информации о координатах узлов. Массив х состоит из одинаковых строк, в которых записаны координаты x1, х2, ..., х6, а массив у содержит одинаковые столбцы с y1, у2, ..., у6. Значения функции в узлах сетки запишем в массив z такой же размерности (6 x 6), причем для вычисления матрицы Z используем выражение для функции, но с поэлементными матричными операциями. Тогда, например z(3,4) как раз будет равно значению функции z(x,y)в точке (х3, у4). Для генерации массивов сетки х и у по координатам узлов в MatLab предусмотрена функция meshgrid, для построения графика в виде каркасной поверхности - функция mesh. Следующие операторы приводят к появлению на экране окна с графиком функции (точка с запятой в конце операторов не ставится для того, чтобы проконтролировать генерацию массивов):

» [X, У] = meshgrid(0:0.2:1,0:0.2:1)
X =
0  0.2000  0.4000  0.6000  0.8000  1.0000
0  0.2000  0.4000  0.6000  0.8000  1.0000
0  0.2000  0.4000  0.6000  0.8000  1.0000
0  0.2000  0.4000  0.6000  0.8000  1.0000
0  0.2000  0.4000  0.6000  0.8000  1.0000
0  0.2000  0.4000  0.6000  0.8000  1.0000
y =
0       0       0       0       0       0
0.2000  0.2000  0.2000  0.2000  0.2000  0.2000
0.4000  0.4000  0.4000  0.4000  0.4000  0.4000
0.6000  0.6000  0.6000  0.6000  0.6000  0.6000
0.8000  0.8000  0.8000  0.8000  0.8000  0.8000
1.0000  1.0000  1.0000  1.0000  1.0000  1.0000

» Z = X.^2+Y.^2

Z =
0  0.0400  0.1600  0.3600  0.6400  1.0000
0.0400  0.0800  0.2000  0.4000  0.6800  1.0400
0.1600  0.2000  0.3200  0.5200  0.8000  1.1600
0.3600  0.4000  0.5200  0.7200  1.0000  1.3600
0.6400  0.6800  0.8000  1.0000  1.2800  1.6400
1.0000  1.0400  1.1600  1.3600  1.6400  2.0000

» mesh(X,Y,Z)

Какие недостатки имеет построенный график? И как их устранить? Построенный график и новый привести в электронном отчете по лабораторной работе.

MatLab позволяет наносить на график дополнительную информацию, в частности, соответствие цветов значениям функции. Сетка генерируется при помощи команды meshgrid, вызываемой с двумя аргументами. Аргументами являются векторы, элементы которых соответствуют сетке на прямоугольной области построения функции. Можно использовать один аргумент, если область построения функции - квадрат. Для вычисления функции следует использовать поэлементные операции.

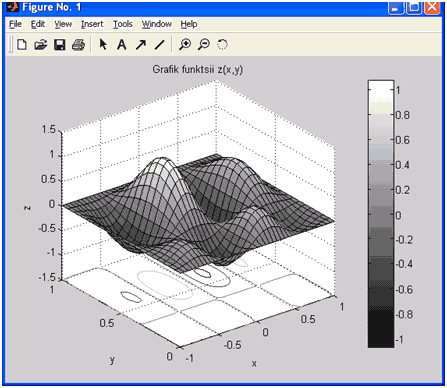
Рассмотрим основные возможности, предоставляемые MatLab для визуализации функций двух переменных, на примере построения графика функции

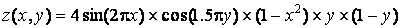
на прямоугольной области определения  х принадлежит [-1, 1],   y [0, 1].
Подготовим матрицы с координатами узлов сетки и значениями функции:

» [X, Y] = meshgrid(-1:0.05:1, 0:0.05:1);
» Z = 4*sin(2*pi*X).*cos(1.5*pi*Y).*(1-Х.^2).*Y.*(1-Y);

Для построения каркасной поверхности используется функция mesh, вызываемая с тремя аргументами:

» mesh(X,Y,Z)

Цвет линий поверхности соответствует значениям функции. MatLab рисует только видимую часть поверхности.

При помощи команды  hidden off можно сделать каркасную поверхность "прозрачной", добавив скрытую часть. Команда  hidden on убирает невидимую часть поверхности, возвращая графику прежний вид.

Функция surf строит каркасную поверхность графика функции и заливает каждую клетку поверхности определенным цветом, зависящим от значений функции в точках, соответствующих углам клетки. В пределах каждой клетки цвет постоянный. Посмотрите результаты выполнения команды

» surf(X,Y,Z)

Команда shading flat позволяет убирать каркасные линии. Для получения поверхности, плавно залитой цветом, зависящим от значений функции, предназначена команда shading interp.
При помощи shading faceted можно вернуться к поверхности с каркасными линиями.
Трехмерные графики, получаемые с помощью описанных выше команд, удобны для получения представления о форме поверхности, однако по ним трудно судить о значениях функции. В MatLab определена команда colorbar, которая выводит рядом с графиком столбик, устанавливающий соответствие между цветом и значением функции. Постройте при помощи surf график поверхности и дополните его информацией о цвете.

» surf(X,Y,Z)
» colorbar

Команду colorbar можно применять в сочетании со всеми функциями, строящими трехмерные объекты.

Пользуясь цветной поверхностью, трудно сделать вывод о значении функции в той или иной точке плоскости xy. Команды meshc или surfc позволяют получить более точное представление о поведении функции. Эти команды строят каркасную поверхность или залитую цветом каркасную поверхность и размещают на плоскости xyлинии уровня функции (линии постоянства значений функции):

» surfc(X,Y,Z)
» colorbar

MatLab позволяет построить поверхность, состоящую из линий уровня, при помощи функции contour3. Эту функцию можно использовать так же, как и описанные выше mesh, surf, meshc и surfc с тремя аргументами. При этом число линий уровня выбирается автоматически. Имеется возможность задать четвертым аргументом в contour3 либо число линий уровня, либо вектор, элементы которого равны значениям функции, отображаемым в виде линий уровня. Задание вектора (четвертого аргумента levels) удобно, когда требуется исследовать поведение функции в некоторой области ее значений (срез функции). Постройте, например поверхность, состоящую из линий уровня, соответствующих значениям функции от  0  до  0.5  с  шагом  0.01:

» levels = [0:0.01:0.5];
» contour3(X, Y, Z, levels)
» colorbar

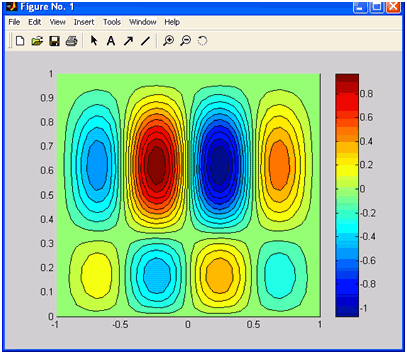
4. Построение контурных графиков функций двух переменных

MatLab предоставляет возможность получать различные типы контурных графиков при помощи функций contour  и  contourf. Рассмотрим их возможности на примере функции

.

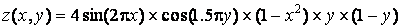Использование contour  с тремя аргументами

» contour(X,Y,Z)

приводит к графику, на котором показаны линии уровня на плоскости xy, но без указания числовых значений на них. Такой график является малоинформативным, он не позволяет узнать значения функции на каждой из линий уровня. Использование команды colorbar также не позволит точно определить значения функции. Каждую линию уровня можно снабдить значением, которое принимает на ней исследуемая функция, при помощи определенной в MatLab функции  clabel. Функция clabel вызывается с двумя аргументами: матрицей, содержащей информацию о линиях уровня и указателем на график, на котором следует нанести разметку. Пользователю не нужно самому создавать аргументы clabel. Функция contour, вызванная с двумя выходными параметрами, не только строит линии уровня, но и находит требуемые для clabel параметры. Используйте contour с выходными аргументами CMatr  и  h (в массиве CMatr содержится информация о линиях уровня, а в массиве h - указатели). Завершите вызов contour точкой с запятой для подавления вывода на экран значений выходных параметров и нанесите на график сетку:

» [CMatr, h] = contour(X, Y, Z);
» clabel(CMatr, h)
» grid on

Дополнительным аргументом функции contour (так же, как и contour3, описанной выше) может быть или число линий уровня, или вектор, содержащий значения функции, для которых требуется построить линии уровня.
Наглядную информацию об изменении функции дает заливка прямоугольника на плоскости xyцветом, зависящим от значения функции в точках плоскости. Для построения таких графиков предназначена функция contourf, использование которой не отличается от применения contour. В следующем примере выводится график, который состоит из двадцати линий уровня, а промежутки между ними заполнены цветами, соответствующими значениям исследуемой функции:

» contourf(X, Y, Z, 20)
» colorbar

5. Оформление графиков функций

Простым и эффективным способом изменения цветового оформления графика является установка цветовой палитры при помощи функции colormap. Следующий пример демонстрирует подготовку графика функции для печати на монохромном принтере, используя палитру gray.

» surfc(X, Y, Z)
»colorbar
» colormap(gray)
» title('График функции z(x,y)')
» xlabel('x')
» ylabel('у')
» zlabel('z')

Обратите внимание, что команда colormap(gray) изменяет палитру графического окна, т.е. следующие графики будут выводиться в этом окне также в серых тонах. Для восстановления первоначального значения палитры следует применить команду colormap('default'). Цветовые палитры, доступные в MatLab, приведены в табл. 2.

Таблица 2

6. Вывод нескольких графиков на одни оси

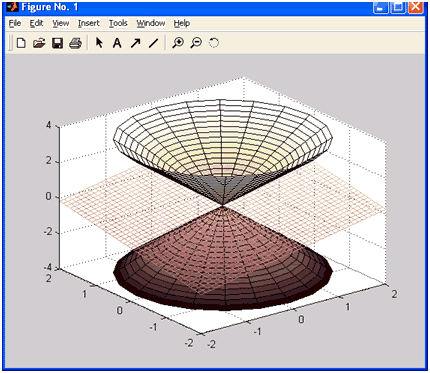
Для отображения нескольких графиков функций одной переменной на одних осях использовались возможности функций plot, plotyy, semilogx, semilogy, loglog. Они позволяют выводить графики нескольких функций, задавая соответствующие векторные аргументы парами, например plot(x,f,x,g). Однако для объединения трехмерных графиков их использовать нельзя. Для объединения таких графиков предназначена команда hold on, которую нужно задать перед построением графика. В следующем примере объединение двух графиков (плоскости и конуса) приводит к их пересечению. Конус задается параметрически следующими зависимостями:

,  ,  ,  .

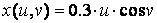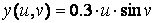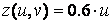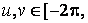
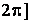Для графического отображения конуса сначала необходимо сгенерировать с помощью двоеточия вектор-столбец и вектор-строку, содержащие значения параметров на заданном интервале (важно, что u - вектор-столбец, а v-вектор-строка):

» u = [-2*pi:0.1*pi:2*pi]';
» v = [-2*pi:0.1*pi:2*pi];

Далее формируются матрицы  X, Y, содержащие значения функци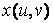й  и 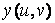 в точках, соответствующих значениям параметров. Формирование матриц выполняется с помощью внешнего произведения векторов.

Замечание 2

Внешним произведением векторов 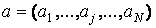,  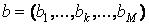называется матрица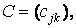  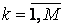  размера  N x M,  элементы которой вычисляются по формуле  .
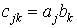Вектор  а  является вектор-столбцом ив MatLab представляется в виде двумерного массива размера N на один. Вектор-столбец bпри транспонировании переходит в вектор-строку размера один на М. Вектор-столбец и вектор-строка есть матрицы, у которых один из размеров равен единице. Фактически, С = abT, где умножение происходит по правилу матричного произведения. Для вычисления матричного произведения в MatLab используется оператор "звездочка". Определим внешнее произведение для двух векторов:

» a = [1;2;3];
» b = [5;6;7];
» C = a*b'
C =
5   6   7
10  12  14
15  18  21

Сформируем матрицы  X,Y, необходимые для графического отображения конуса:

» X = 0.3*u*cos(v);
» Y = 0.3*u*sin(v);

Матрица Z должна быть того же размера, что и матрицы  X иY. Кроме того, она должна содержать значения, соответствующие значениям параметров. Если бы в функцию 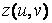 входило произведение и  и  v, то матрицу Z можно было заполнить аналогично матрицам Xи Yпри помощи внешнего произведения. С другой стороны, функцию z(u,v)можно представить в ви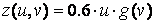де , где 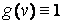. Поэтому для вычисления Zможно применить внешнее произведение векторов  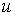и 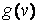, где вектор-строка  имеет ту же размерность, что v, но состоит из единиц:

» Z = 0.6*u*ones(size(v));

Все требуемые матрицы для отображения конуса созданы. Задание плоскости выполняется следующим образом:

» [X,Y] = meshgrid(-2:0.1:2);
» Z = 0.5*X+0.4*Y;

Теперь не сложно записать и полную последовательность команд для построения пересекающихся конуса и плоскости:

» u = [-2*pi:0.1*pi:2*pi]';
» v = [-2*pi:0.1*pi:2*pi];
» X = 0.3*u*cos(v);
» Y = 0.3*u*sin(v);
» Z = 0.6*u*ones(size(v));
» surf(X, Y, Z)
» [X,Y] = meshgrid(-2:0.1:2);
» Z = 0.5*X+0.4*Y;
» hold on
» mesh(X, Y, Z)
» hidden off

Команда hidden off применена для того, чтобы показать часть конуса, находящуюся под плоскостью.
Обратите внимание, что команда hold on распространяется на все последующие выводы графиков в текущее окно. Для размещения графиков в новых окнах следует выполнить команду hold off. Команда hold on может применяться и для расположения нескольких графиков функций одной переменной, например,

» plot(x,f,х,g)

эквивалентно последовательности

» plot(х,f)
» hold on
» plot(x,g)

Результаты работы, полученные мною: