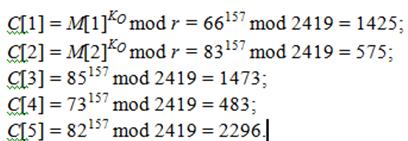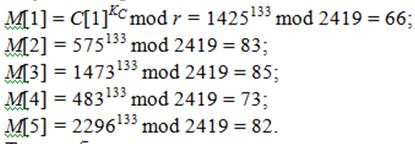Криптосистема RSA была предложена в 1977 году тремя учёными: Роном Ривестом, Ади Шамиром и Леонардом Адлеманом. Алгоритм шифрования данных RSA является асимметричным, поскольку для шифрования и расшифрования данных используются два различных ключа, называемых открытым и закрытым. Принципиальное отличие криптосистемы RSA от симметричных криптосистем заключается в том, что раскрытие ключа, которым было произведено шифрование, не влечёт за собой раскрытия исходного текста. Данный факт допускает пересылку ключа шифрования без использования каких-либо защищённых каналов связи. Это обеспечивается свойством криптосистемы RSA, в соответствии с которым использованный для шифрования данных открытый ключ не подходит для их расшифрования. Для расшифрования используется закрытый ключ, который не может быть получен из открытого.
Шифрование в системе RSA производится путём возведения исходного текста X (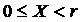
) в степень открытого ключа KО по модулю большого числа r:
Y = EKO(X) =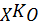 
mod r. (13)
Расшифрование производится путём возведения шифротекста Y в степень закрытого ключа KС по модулю r :
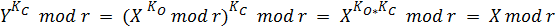. (14)
Возможность получения исходного текста из зашифрованного обеспечивается свойством открытого и закрытого ключей, для которых должно выполняться равенство
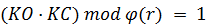, (15)
где 
– функция Эйлера от r. Закрытый ключ является мультипликативным инверсным по модулю 
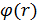для открытого. По теореме Эйлера
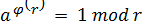, (16)
где (a, r) = 1.
Известно, что если
a = b mod r, (17)
то
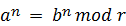. (18)
Из этого следует, что
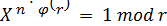. (19 )
Поскольку для модулярной арифметики справедливо
m*a = m*b mod r,
то мы можем умножить левую и правую части равенства (19) на X:
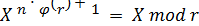. (20)
Если представить показатель степени n*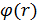+1 как произведение значений KO и KC, то получим
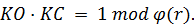(21)
Процедура формирования параметров алгоритма RSA выглядит следующим образом:
1) генерируются два больших простых числа: p и q,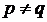 
;
2) вычисляется произведение данных чисел: r = p*q;
3) находится функция Эйлера от r: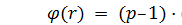 
;
4) генерируется значение открытого ключа KO, исходя из следующих условий: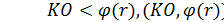 
;
5) вычисляется мультипликативное инверсное по модулю 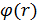для KO. Полученное значение будет являться закрытым ключом KC .
Для вычисления мультипликативного инверсного можно использовать расширение алгоритма Евклида. Расширенный алгоритм Евклида позволяет найти значения x1 и y1, при которых выполняется равенство x1*a + y1*b = d1, где
d1 = НОД(a, b). Если a > b и числа a, b – взаимно простые, т. е. d1 = 1, то y1 является мультипликативным инверсным для b по модулю а.
EUCLIDEX(a; b)
d0:=a; d1:=b;
x0:=1; x1:=0;
y0:=0; y1:=1;
while d1>1 do
begin
q:=d0 div d1;
d2:=d0 mod d1;
x2:=x0–q*x1;
y2:=y0–q*y1;
d0:=d1; d1:=d2;
x0:=x1; x1:=x2;
y0:=y1; y1:=y2;
end
return (x1; y1; d1)
Если расширенный алгоритм Евклида используется для вычисления мультипликативного инверсного и в результате выполнения алгоритма получено отрицательное значение, то к нему необходимо прибавить величину а.
Для выполнения процедур шифрования и расшифрования можно использовать алгоритм быстрого возведения в степень по модулю, позволяющий для положительных целых a, z и n вычислить x = az mod n.
FASTEXP(a; z; n)
a1:=a; z1:=z; x:=1;
while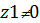 
do
begin
while (z1 mod 2)=0 do
begin
z1:=z1 div 2;
a1:=(a1*a1) mod n;
end
z1:=z1–1;
x:=(x*a1) mod n;
end
return (x)
Рассмотрим пример использования алгоритма RSA:
1) выберем два простых числа: p = 41 и q = 59;
2) вычислим их произведение q = p*q = 2419;
3) вычислим функцию Эйлера: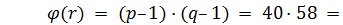 
;
4) выберем КО = 157; (2320, 157) = (157, 122) = (122, 35) = (35, 17) = 1;
5) найдем значение КС, для которого выполняется:
.
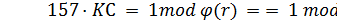Положив а равным 
и b равным KО, по расширенному алгоритму Евклида вычислим КС = y1 = 133.
В качестве примера зашифруем строку «BSUIR». Символам исходного текста соответствуют следующие десятичные ASCII-коды:
«B» : 66;
«S» : 83;
«U» : 85;
«I» : 73;
«R» : 82.
Таким образом, исходный текст M будет представлять собой последовательность чисел: M={66, 83, 85, 73, 82}. Тогда компоненты шифротекста C будут получены следующим образом:
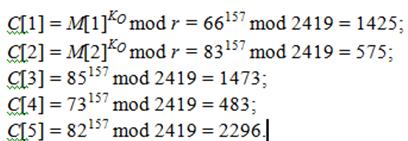
Для расшифрования шифротекста C={1425, 575, 1473, 483, 2296} воспользуемся закрытым ключом KC:
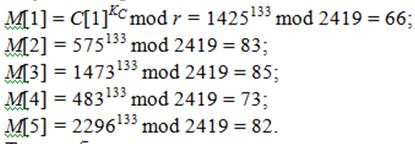
Таким образом, мы вновь получили исходный текст {66, 83, 85, 73, 82}, который соответствует строке «BSUIR».
Субъект, желающий получать зашифрованные по алгоритму RSA сообщения, публикует сгенерированную им пару значений (КО, r) в общедоступном месте. Значение закрытого ключа КС, а также значения p и q хранятся в секрете.
Для того чтобы организовать секретный канал связи, абоненты A и B посылают друг другу свои открытые ключи, не заботясь о том, что их значения узнает кто-то посторонний. При обмене сообщениями абонент A шифрует отправляемые данные открытым ключом абонента B, а абонент B шифрует отправляемые данные открытым ключом абонента A. Для расшифрования полученных сообщений участники переписки используют свои секретные ключи.
Криптостойкость системы RSA основывается на сложности определения закрытого ключа по открытому, поскольку для этого потребуется вычислить функцию Эйлера от значения параметра r,для чего необходимо разложить r на множители. На сегодняшний день данная задача не имеет эффективного решения, а использование традиционных методов поиска множителей для чисел размерностью порядка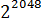 
(именно такие числа рекомендуется использовать в алгоритме RSA) не позволяет осуществить взлом криптосистемы за разумное время.
Автор: Ярмолик, В. Н.
