Алгоритм сложения неотрицательных чисел достаточно прост: цифры числа складываются, начиная с младших разрядов к старшим. Если зафиксировано переполнение (т. е. при сложении получена цифра, большая максимально возможной в данной системе счисления), то происходит перенос значения в следующий разряд. Рассмотрим реализацию сложения неотрицательных n-разрядных целых чисел (un-1, …, u0)b и (vn-1, …, v0)b по основанию b. Следующий алгоритм формирует их сумму (wn, wn-1, …, w0)b, причем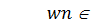 
:
ADD(u, v, n)
j := 0; k := 0;
while j < n
do wj := uj + vj + k
if wj >= b
then wj := wj – b
k := 1
else k := 0
j := j + 1
wn := k
return (wn, …, w0)
Заметим, что при работе этого алгоритма всегда выполняются соотношения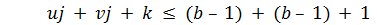 
, так что размер результата суммирования не превышает 
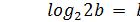разрядов. Приведенный алгоритм может использоваться и для сложения отрицательных чисел. Для этого следует использовать их представление в дополнительном коде.
Автор: Ярмолик, В. Н.
