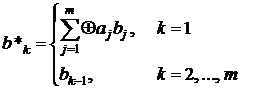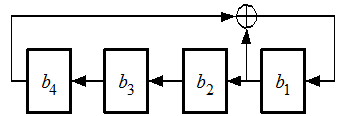Основная идея потоковых криптосистем заключается в шифровании исходного текста M с помощью криптографического ключа K, длина которого равна длине текста. Каждый бит шифротекста Ci является функцией соответствующих битов исходного текста и ключевого потока:
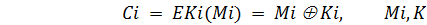
При дешифровании выполняется обратное преобразование DKi:
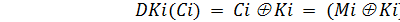
Символом « » обозначена операция сложения «ИСКЛЮЧАЮЩЕЕ-ИЛИ». Благодаря линейным свойствам этой операции при шифровании и дешифровании используется одинаковый ключевой поток K. Очевидно, что в этом случае длина K должна быть равна длине передаваемого сообщения. Однако обмен ключами большого размера зачастую невозможен. Поэтому на практике для формирования ключевого потока используют генераторы псевдослучайной последовательности (рис. 1). Начальные параметры I генераторов на стороне отправителя и получателя должны совпадать, они являются секретным ключом алгоритма. Псевдослучайная последовательность каждого генератора обладает определенным периодом, после которого значения повторяются. Поэтому необходимо выбирать такие генераторы ключа, чтобы этот период превышал длину шифруемой информации.
» обозначена операция сложения «ИСКЛЮЧАЮЩЕЕ-ИЛИ». Благодаря линейным свойствам этой операции при шифровании и дешифровании используется одинаковый ключевой поток K. Очевидно, что в этом случае длина K должна быть равна длине передаваемого сообщения. Однако обмен ключами большого размера зачастую невозможен. Поэтому на практике для формирования ключевого потока используют генераторы псевдослучайной последовательности (рис. 1). Начальные параметры I генераторов на стороне отправителя и получателя должны совпадать, они являются секретным ключом алгоритма. Псевдослучайная последовательность каждого генератора обладает определенным периодом, после которого значения повторяются. Поэтому необходимо выбирать такие генераторы ключа, чтобы этот период превышал длину шифруемой информации.

Рис. 1 . Схема потоковой криптосистемы
Для корректной работы потоковых криптосистем необходимо, чтобы передающая и принимающая сторона имели синхронизированные генераторы ключа K. Искажение отдельных символов не влияет на расшифровку остальных символов шифротекста. Добавление, удаление или дублирование символов шифротекста нарушает синхронизацию ключевой и текстовой последовательностей, и все последующие символы расшифровываются некорректно.
Рассмотрим генераторы ключей на основе сдвиговых регистров с линейной обратной связью LFSR (Linear Feedback Shift Register). Они достаточно просто реализуются в программном и аппаратном виде, обладают высокой скоростью генерации и большим периодом ключа. Регистр LFSR состоит из двух частей: сдвигового регистра, выполняющего сдвиг своих разрядов влево на один разряд, и функции обратной связи, вычисляющей вдвигаемое в первый разряд значение. В обобщенном виде структура LFSR представлена на рис. 2.
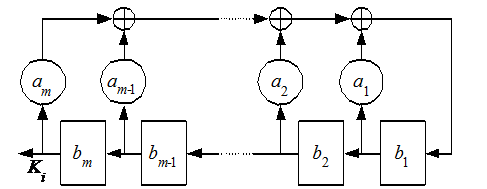
Рис. 2 . Обобщенная схема LFSR
Структуру конкретного регистра LFSR принято задавать с помощью характеристического (задающего) многочлена:
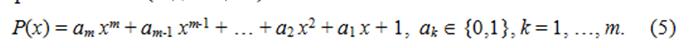
Степень многочлена m задает длину сдвигового регистра. Ненулевые коэффициенты ak определяют разряды регистра, которые будут участвовать в формировании вдвигаемого в первый разряд значения. Через 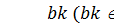 ) обозначены текущие значения разрядов LFSR (k = 1, …, m). Новые значения разрядов
) обозначены текущие значения разрядов LFSR (k = 1, …, m). Новые значения разрядов 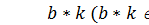 ) вычисляются по следующему закону:
) вычисляются по следующему закону:
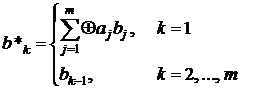 |
– функция обратной связи |
(6) |
– сдвиг. |
Таким образом, новое значение для всех разрядов, кроме первого, берется из ближайшего младшего разряда. Символом 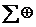 обозначена многоместная операция сложения «ИСКЛЮЧАЮЩЕЕ-ИЛИ». Она используется для сложения значений из разрядов, которые отмечены ненулевыми коэффициентами ak характеристического многочлена. Полученная сумма вдвигается в первый разряд LFSR. Очередной бит ключа Ki для потоковой криптосистемы равен значению старшего разряда LFSR bm.
обозначена многоместная операция сложения «ИСКЛЮЧАЮЩЕЕ-ИЛИ». Она используется для сложения значений из разрядов, которые отмечены ненулевыми коэффициентами ak характеристического многочлена. Полученная сумма вдвигается в первый разряд LFSR. Очередной бит ключа Ki для потоковой криптосистемы равен значению старшего разряда LFSR bm.
Пример 1. Построим сдвиговый регистр с линейными обратными связями, задаваемый характеристическим многочленом P(x) = x4 + x + 1.
Схема регистра приведена на рис. 3. Если начальное состояние регистра I = 1111, то последовательность генерируемых состояний имеет вид
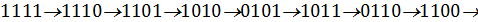
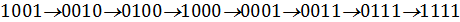
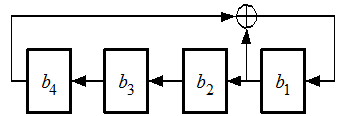
Рис. 3 . LFSR на основе многочлена 
Последнее состояние совпадает с начальным, после этого указанная последовательность повторяется. Последовательность сгенерированных бит ключа: 1111010110010001.
Свойства генерируемой последовательности определяются постоянными коэффициентами характеристического многочлена ai. При их соответствующем выборе генерируемая последовательность K будет иметь максимально возможный период, равный  – 1. Последовательность максимально возможного для данного генератора периода называется M-последовательностью. Основная задача синтеза генератора на основе LFSR – нахождение характеристического многочлена, позволяющего сформировать М-последовательность. Для того чтобы конкретный LFSR имел максимальный период, соответствующий многочлен должен быть примитивным. В общем случае не существует простого способа нахождения примитивных многочленов данной степени, проще выбирать многочлен случайным образом и проверять, является ли он примитивным. Эта задача аналогична задаче проверки на простоту случайно выбранного целого числа и решается с помощью вычислительной техники. Табл. 1 содержит некоторые примитивные многочлены.
– 1. Последовательность максимально возможного для данного генератора периода называется M-последовательностью. Основная задача синтеза генератора на основе LFSR – нахождение характеристического многочлена, позволяющего сформировать М-последовательность. Для того чтобы конкретный LFSR имел максимальный период, соответствующий многочлен должен быть примитивным. В общем случае не существует простого способа нахождения примитивных многочленов данной степени, проще выбирать многочлен случайным образом и проверять, является ли он примитивным. Эта задача аналогична задаче проверки на простоту случайно выбранного целого числа и решается с помощью вычислительной техники. Табл. 1 содержит некоторые примитивные многочлены.
Таблица 1
Примитивные многочлены

Использование LFSR для создания потоковых криптосистем предполагает наличие уязвимости, связанной с линейным характером генерируемой последовательности. Обладая парой «исходный текст – шифротекст» длиной всего 2m бит, взломщик может восстановить характеристический многочлен и дешифровать все сообщение. Для защиты от этой атаки следует увеличивать размер используемого LFSR или использовать более сложные схемы генерации ключа. Рассмотрим, для примера, генератор Геффе (Geffe), представленный на рис. 4.

Рис. 4 . Генератор Геффе
В нем используются три регистра с линейной обратной связью, объединённые нелинейным образом. Два регистра LFSR являются входами мультиплексора, а третий – управляет его выходом. Через x1, x2 и x3 обозначены выходы трёх LFSR, выход генератора Геффе xG описывается так: xG = (x1 and x2) or
(not x1 and x3). Период данного генератора равен 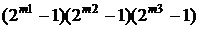 , где m1, m2 и m3 – длины первого, второго и третьего LFSR соответственно.
, где m1, m2 и m3 – длины первого, второго и третьего LFSR соответственно.
Благодаря простоте реализации, высокой скорости работы и сравнительно высокой криптостойкости потоковые шифраторы получили широкое распространение для шифрования информации средней степени секретности. Например, алгоритм A5, построенный на основе трех LFSR с прореженными обратными связями, входит в состав стандарта мобильной связи GSM.
Возможны и другие способы генерации ключевой последовательности. Например, генератор ключевого потока K в алгоритме RC4 работает на основе подстановочной таблицы S (S-бокса) из 256 символов. На первом шаге S-бокс заполняется линейно: S[0] = 0, S[1] = 1, …, S[255] = 255. Затем начальное значение S-бокса меняется на основе пользовательского секретного ключа U по следующему алгоритму:
j := 0;
for i := 0 to 255
j := (j + S[i] + U[i mod length(U)]) mod 256;
swap(S[i], S[j]);
Эта подстановка является функцией от ключа изменяемой длины. Процедура swap меняет местами значения таблицы S с заданными индексами.
Полученное значение S-бокса используется для побайтной генерации ключевого потока K. Генератор потока имеет два счетчика i и j, инициализируемых нулевым значением. На каждом шаге генерации выполняются следующие операции:
i := (i + 1) mod 256
j := (j + S[i]) mod 256
swap(S[i], S[j])
K := S[(S[i] + S[j]) mod 256]
Байт K складывается операцией «ИСКЛЮЧАЮЩЕЕ-ИЛИ» с байтом открытого текста для получения байта шифротекста либо с байтом шифротекста для получения байта исходного текста. Шифрование происходит весьма быстро – примерно в 10 раз быстрее DES-алгоритма. Типичная реализация выполняет 19 машинных команд на каждый байт текста. Алгоритм RC4 может принимать примерно 256!* 2562 = 21700 возможных состояний. S-бокс медленно изменяется в процессе работы: параметр i обеспечивает изменение каждого элемента, а j отвечает за то, чтобы эти элементы изменялись случайным образом. Шифр обладает иммунитетом к методам линейного и дифференциального криптоанализа и до сих пор в нем не обнаружены короткие циклы.
Алгоритм RC4, в отличие от алгоритмов на основе сдвиговых регистров LSFR, больше ориентирован на программную реализацию, поскольку работает не с битами, а с целыми байтами исходного текста. Благодаря своей скорости и защищенности, он нашел широкое применение в криптографических системах. Например, он является частью протокола безопасного обмена информацией SSL.
Автор: Ярмолик, В. Н.