Эллиптическая кривая над множеством действительных чисел может быть определена как набор точек (x, y), удовлетворяющих уравнению эллиптической кривой вида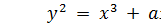 (x, y, a и b – действительные числа), а также некоторый элемент O, называемый неопределенным (нулевым) элементом (рис. 15).
(x, y, a и b – действительные числа), а также некоторый элемент O, называемый неопределенным (нулевым) элементом (рис. 15).

Рис. 15 . Эллиптическая кривая 
По определению, эллиптическая кривая обладает следующим свойством: если три ее точки лежат на одной прямой, то их сумма равна O. Это свойство позволяет описать правила сложения и умножения точек эллиптической кривой.
- Если O – нулевой элемент, то справедливо равенство O = –O, а для любой точки P эллиптической кривой имеем P + O = P.
- Прямая, проходящая через точки P и –P, является вертикальной прямой, которая не пересекает эллиптическую кривую ни в какой третьей точке. По определению, Р + (–Р) = О.
- Пусть P и Q – две различные точки эллиптической кривой, и Р не равно –Q. Проведем через P и Q прямую. Она пересечет эллиптическую кривую только еще в одной точке, называемой –R. Точка –R отображается относительно оси Х в точку R. Закон сложения: P + Q = R.
- Чтобы сложить точку Р с ней самой, нужно провести касательную к кривой в точке Р. Если
 , то касательная пересечет эллиптическую кривую ровно в одной точке R. Закон удвоения точки Р: P + P = 2P = R.
, то касательная пересечет эллиптическую кривую ровно в одной точке R. Закон удвоения точки Р: P + P = 2P = R.
- Умножение точки Р на целое положительное k определяется как сумма k точек Р: kP = P + P + P + … + P.
Эллиптическая кривая может быть использована для построения эллиптической группы, если ее параметры a и b удовлетворяют соотношению 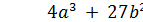 (mod M), где М – простое число, a < M и b < M.
(mod M), где М – простое число, a < M и b < M.
Эллиптическая группа EM(a,b) представляет собой набор точек (x, y) с целыми положительными координатами, x < М и y < М, которые удовлетворяют соотношению 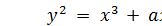 (mod M).
(mod M).
Алгоритм формирования элементов эллиптической группы:
- Для всех значений x (0 < x < M) вычисляется значение
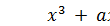 (mod M).
(mod M).
- Для каждого значения из шага 1 определяется квадратный корень по модулю M и элемент включается в группу EM(a,b), если результат положительный.
Пример. Пусть a = 1, b = 0 и M = 23, тогда 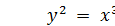 . Так как
. Так как
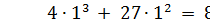 (mod 23), то можно построить группу E23(1,1). Существуют 23 точки, которые удовлетворяют уравнению группы, а именно (0,0) (1,5) (1,18) (9,5) (9,18) (11,10) (11,13) (13,5) (13,18) (15,3) (15,20) (16,8) (16,15) (17,10) (17,13) (18,10) (18,13) (19,1) (19,22) (20,4) (20,19) (21,6) (21,17). Заметим, что для каждого значения x существует по две точки с симметрией относительно у = 11,5. В случае эллиптических кривых над действительными числами для каждой точки имеется отрицательная, отображаемая относительно оси х. В случае использования конечной эллиптической группы отрицательные значения координаты y берутся по модулю, в результате чего получаются положительные координаты: –P = (xP, (–yP mod M)). Например, если P = (1,5), то
(mod 23), то можно построить группу E23(1,1). Существуют 23 точки, которые удовлетворяют уравнению группы, а именно (0,0) (1,5) (1,18) (9,5) (9,18) (11,10) (11,13) (13,5) (13,18) (15,3) (15,20) (16,8) (16,15) (17,10) (17,13) (18,10) (18,13) (19,1) (19,22) (20,4) (20,19) (21,6) (21,17). Заметим, что для каждого значения x существует по две точки с симметрией относительно у = 11,5. В случае эллиптических кривых над действительными числами для каждой точки имеется отрицательная, отображаемая относительно оси х. В случае использования конечной эллиптической группы отрицательные значения координаты y берутся по модулю, в результате чего получаются положительные координаты: –P = (xP, (–yP mod M)). Например, если P = (1,5), то
–P = (1, (–5 mod 23)) = (1,18).
Рассмотрим алгоритм сложения точек эллиптической группы. Пусть
Р = (x1, y1) и Q = (x2, y2). Тогда P + Q = (x3, y3), где 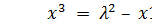 (mod M) и
(mod M) и
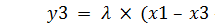 (mod M), а
(mod M), а
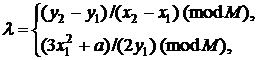 |
если P 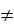 Q, Q, |
(27) |
если P = Q. |
Число  – угловой коэффициент секущей, проведенной через точки
– угловой коэффициент секущей, проведенной через точки
Р = (x1,y1) и Q = (x2, y2). При Р = Q секущая превращается в касательную, чем и объясняется наличие двух формул для вычисления  .
.
Пример. Эллиптическая группа задана уравнением 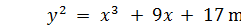 . Необходимо найти произведение 2P=P+P для точки P = (16, 5) из этой группы
. Необходимо найти произведение 2P=P+P для точки P = (16, 5) из этой группы
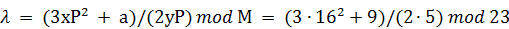 ;
;
тогда 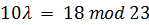 , отсюда
, отсюда
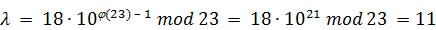 ;
;
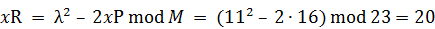 ;
;
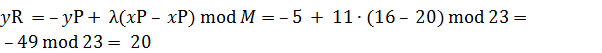 .
.
В результате получаем 2P = (20,20).
Умножение точек эллиптической группы на число определяется аналогично умножению для эллиптических кривых как многократное сложение точки с собой. Если вычислять P + P + P + … достаточно долго, то, т.к. число точек конечно, в конце концов должен быть получен результат O. Всегда можно найти такие a и b (b > a), что aP = bP. Это означает, что cP = O , где c = b – a. Наименьшее c, для которого это справедливо, называется порядком точки.
Использование эллиптических групп в криптографических целях основано на сложности решения задачи дискретного логарифмирования в эллиптической группе, которая может быть сформулирована так: для заданных точек P и Q найти такое k, чтобы kP = Q. Значение k называется логарифмом от Q по основанию P. Если взять значение k достаточно большим, то задача нахождения k становится практически неосуществимой.
Читайте про:
Автор: Ярмолик, В. Н.


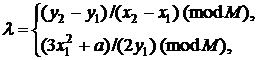
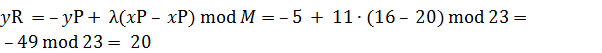 .
.