Простейшие шифры подстановки (substitution) реализуют замену каждого символа исходного текста на один из символов алфавита шифротекста. В общем случае подстановочный шифр описывается таблицей подстановки, состоящей из двух строк и n столбцов. Количество столбцов таблицы подстановки соответствует количеству различных символов в алфавите исходного текста. Верхняя строка таблицы подстановки содержит все возможные символы исходного текста, а нижняя – соответствующие им символы шифротекста.
Моноалфавитные шифры характеризуются однозначным соответствием символов исходного текста и символов шифротекста. В случае когда алфавиты исходного текста и шифротекста состоят из одного и того же множества символов, алфавит шифротекста представляет собой простую перестановку лексикографического порядка символов в алфавите исходного текста. При выполнении шифрования каждый символ исходного текста заменяется соответствующим ему символом шифротекста.
Таблица подстановки, описывающая моноалфавитный шифр, преобразующий строчные буквы русского алфавита, будет состоять из 33 столбцов, что соответствует количеству букв в алфавите. Рассмотрим такую таблицу на следующем примере:

В соответствии с приведённой таблицей шифрование строки
«знание – сила» будет выполнено следующим образом:
«з» --> «ш»;
«н» --> «ф»;
…
«a» --> «e».
В результате шифрования будет получен шифротекст «шфефуи – оусе».
Таблица подстановки, описывающая ключ моноалфавитного шифра, преобразующего ASCII-коды (однобайтовые значения), будет состоять из 256 столбцов. Таблица подстановки для шифра, осуществляющего подстановку 32-битных значений, будет состоять из 232 столбцов, что уже вызовет сложности её хранения и передачи. По этой причине на практике вместо таблиц подстановок используются функции подстановки, аналитически описывающие соответствие между порядковыми номерами символов исходного текста в алфавите исходного текста и порядковыми номерами символов шифротекста в алфавите шифротекста.
Предположим, алфавит исходного текста М состоит из n символов
М={a0, a1, ..., an}, тогда алфавит шифротекста C будет представлять собой
n-символьный алфавит С={f(a0), f(a1), ..., f(an)}, где функция f, выполняющая отображение М-->C, и будет являться функцией подстановки. В общем случае функция подстановки любого моноалфавитного шифра может быть задана в виде полинома степени t:
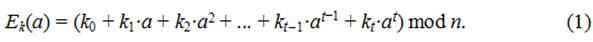
Примером простейшего моноалфавитного шифра является шифр Цезаря. Строки таблицы подстановки для шифра Цезаря представляют собой сдвинутые друг относительно друга на l позиций алфавиты исходного текста. Сам Цезарь использовал для шифрования величину сдвига l = 3. Функция подстановки для шифра Цезаря будет задаваться полиномом нулевой степени:
Ek(a) = (a + k) mod n. (2)
Поскольку для моноалфавитных шифров каждый символ исходного текста при шифровании может заменяться одним единственным символом шифротекста, для криптоанализа данных шифров возможно применение анализа частот встречаемости символов в шифротексте. Данная атака основана на том факте, что в естественных языках частоты встречаемости различных букв могут существенно отличаться. Так, в английском языке наиболее часто встречаемой является буква «e», а наименее встречаемой – буква «z». Зная типичную частоту встречаемости каждого из символов алфавита исходного текста, можно воссоздать использованную при шифровании таблицу постановки, ставя каждому из символов исходного текста в соответствие символ шифротекста, частота встречаемости которого в зашифрованном тексте является наиболее близкой к типичной частоте встречаемости символа алфавита исходного текста.
Подстановочные шифры, называемые полиалфавитными, используют более чем одну таблицу подстановки. Использование нескольких таблиц (алфавитов) обеспечивает возможность нескольких вариантов подстановки символов исходного сообщения, что повышает криптостойкость шифра.
Классическим полиалфавитным шифром является шифр Виженера (Vigenere Cipher). Так же как и в случае шифра Цезаря, данный шифр может быть задан таблицами подстановки, состоящими из n столбцов, где n – размер алфавита исходного текста. Количество таблиц подстановки для случая шифра Виженера будет равняться m, где m – длина ключевого слова (период ключа). Ключевое слово задаёт количество символов, на которое смещены относительно исходного алфавиты шифротекста в каждой из m таблиц подстановок.
Рассмотрим работу шифра Виженера на простом примере. Пусть дано ключевое слово «MOUSE». Тогда правила подстановки будут задаваться 5-ю таблицами, которые для компактности можно объединить в одну.
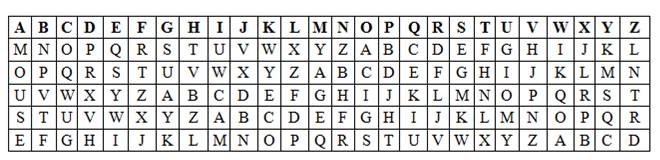
Пусть необходимо зашифровать текст «CRYPTOGRAPHY AND DATA SECURITY». Сперва запишем символы ключевого слова под символами исходного текста. Поскольку ключ в методе Виженера – периодический, повторим ключевое слово столько раз, сколько нам потребуется, чтобы закрыть весь исходный текст.
CRYPTOGRAPHY AND DATA SECURITY
MOUSEMOUSEMOUSEMOUSEMOUSEMOUSE
Каждый из символов ключа указывает, которую из таблиц подстановки нам необходимо использовать для подстановки рассматриваемого символа исходного текста. Символ ключа «M» указывает, что соответствующий символ шифротекста необходимо выбирать из таблицы подстановки, алфавит шифротекста в которой сдвинут относительно алфавита исходного текста на
Pos(«M») – Pos(«A») = 12 позиций. Таким образом, первому символу исходного текста будет соответствовать символ шифротекста «C». Проведя аналогичную процедуру для всех символов исходного текста, получим искомый шифротекст:
«OFSHXAULSTTM SRP XSXM MWGGFCLC».
Как видно из примера, в результате шифрования по методу Виженера символы исходного текста «P» и «H» были преобразованы в один и тот же подстановочный элемент «T». Таким образом, отсутствует однозначное соответствие между символами исходного и зашифрованного текстов, что делает применение атаки на шифротекст путём частотного анализа «в лоб» невозможным.
Поскольку ключ шифратора Виженера является периодическим, зашифрованный текст можно представить как m текстов, зашифрованных по методу Цезаря. В рассмотренном примере для текста «CRYPTOGRAPHY AND DATA SECURITY» символы с позициями 1, 6, ..., 26 шифровались по методу Цезаря с ключом k = 12; символы с позициями 2, 7, ..., 27 – ключом k = 14; с позициями 3, 8, ..., 28 – ключом k = 20; с позициями 4, 9, ..., 29 – ключом k = 18; с позициями 5, 10, ..., 30 – ключом k = 4.

Таким образом, зная длину ключевого слова шифра Виженера (период ключа), можно произвести взлом шифротекста, выполнив анализ частот встречаемости символов в отдельности для каждого из m компонентов шифротекста.
Одним из методов определения длины ключевого слова, использованного при шифровании текста по методу Виженера, является метод Касиски (Kasiski).
Данный метод основан на предположении, что наличие повторяющихся l-грамм (l-символьных последовательностей) в зашифрованном тексте будет в большинстве случаев обусловлено наличием соответствующих повторяющихся l-грамм в исходном тексте. Предполагается, что случайное появление в шифротексте повторяющихся l-грамм маловероятно.
Одинаковым l-граммам, присутствующим в исходном тексте, будут соответствовать одинаковые l-граммы, расположенные на тех же позициях в шифротексте, только в том случае, если при шифровании они будут преобразованы с использованием тех же l символов ключа. Это условие будет выполняться для всех повторяющихся l-грамм, расположенных друг от друга на расстояниях, кратных длине ключевого слова шифра.
Тест Касиски состоит из следующих шагов:
- Анализируется шифротекст на предмет присутствия в нём повторяющихся l-грамм.
- Для каждой из встретившихся в шифротексте более одного раза
l-граммы вычисляются расстояния между её соседними вхождениями.
- Вычисляется наибольший общий делитель полученного на предыдущем шаге множества расстояний с учётом того, что среди найденных повторений l-грамм могут в незначительном количестве присутствовать случайные повторения. Полученное значение и будет являться длиной ключевого слова.
Эксперименты показывают, что данный метод является достаточно эффективным при анализе зашифрованных текстов на русском и английском языках в случае, если в тексте присутствуют повторяющиеся l-граммы длиной в три и более символов.
Автор: Ярмолик, В. Н.



