1. Логическая структура
Массив - такая структура данных, которая характеризуется:
- фиксированным набором элементов одного и того же типа;
- каждый элемент имеет уникальный набор значений индексов;
- количество индексов определяют мерность массива, например, два индекса - двумерный массив, три индекса - трехмерный массив, один индекс - одномерный массив или вектор;
- обращение к элементу массива выполняется по имени массива и значениям индексов для данного элемента.
Другое определение: массив - это вектор, каждый элемент которого - вектор.
Синтаксис описания массива представляется в виде:
<Имя> : Array [n1..k1] [n2..k2] .. [nn..kn] of <Тип>.
Для случая двумерного массива:
Mas2D : Array [n1..k1] [n2..k2] of <Тип>, или
Mas2D : Array [n1..k1 , n2..k2] of <Тип>
Наглядно двумерный массив можно представить в виде таблицы из (k1-n1+1) строк и (k2-n2+1) столбцов.
2. Физическая структура
Многомерные массивы хранятся в непрерывной области памяти. Количество элементов массива и размер элемента определяют размер памяти для хранения массива. Принцип распределения элементов массива в памяти определен языком программирования. Так в FORTRAN элементы распределяются по столбцам - так, что быстрее меняется левые индексы, в Pascal - по строкам - изменение индексов выполняется в направлении справа налево.
Количество байтов памяти, занятых двумерным массивом, определяется по формуле :
ByteSize = (k1-n1+1)*(k2-n2+1)*SizeOf(Тип) (3.3)
Адресом массива является адрес первого байта начального компонента массива. Смещение к элементу массива Mas[i1,i2] определяется по формуле:
ByteNumber = [(i1-n1)*(k2-n2+1)+(i2-n2)]*SizeOf(Тип) (3.4)
его адрес : @ByteNumber = @mas + ByteNumber.
3. Операции
Важнейшая операция физического уровня над массивом - доступ к заданному элементу. Как только реализован доступ к элементу, над ним может быть выполнена любая операция, имеющая смысл для того типа данных, которому соответствует элемент. Преобразование логической структуры в физическую, в ходе которого многомерная логическая структура массива преобразуется в одномерную физическую структуру, называется процессом линеаризации.
В соответствии с формулами (3.3), (3.4) и по аналогии с вектором (3.1), (3.2) для двумерного массива с границами изменения индексов:
[B(1)..E(1)][B(2)..E(2)], размещенного в памяти по строкам, адрес элемента с индексами [I(1),I(2)] может быть вычислен как:
Addr[I(1),I(2)] = Addr[B(1),B(2)] +{ [I(1)-B(1)] * [E(2)-B(2)+1] + [I(2)-B(2)] }*SizeOf(Тип) (3.5)
Обобщая (3.5) для массива произвольной размерности:
Mas[B(1)..E(2)][B(2)..E(2)]...[B(n)..E(n)]
получим:
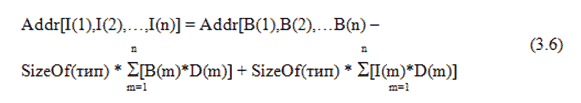
где Dm зависит от способа размещения массива. При размещении по строкам:
D(m)=[E(m+1)-B(m+1)+1]*D(m+1), где m = n-1,...,1 и D(n)=1
при размещении по столбцам:
D(m)=[E(m-1)-B(m-1)+1]*D(m-1), где m = 2,...,n и D(1)=1
При вычислении адреса элемента наиболее сложным является вычисление третьей составляющей формулы (3.6), т.к. первые две не зависят от индексов и могут быть вычислены заранее. Для ускорения вычислений множители D(m) также могут быть вычислены заранее и сохраняться в дескрипторе массива. Дескриптор массива, таким образом, содержит:
- начальный адрес массива - Addr[I(1),I(2),...,I(n)];
- число измерений в массиве - n;
- постоянную составляющую формулы линеаризации (первые две составляющие формулы (3.6);
- для каждого из n измерений массива:
- значения граничных индексов - B(i), E(i);
- множитель формулы линеаризации - D(i).
4. Специальные массивы
На практике встречаются массивы, которые в силу определенных причин могут записываться в память не полностью, а частично. Это особенно актуально для массивов настолько больших размеров, что для их хранения в полном объеме памяти может быть недостаточно. К таким массивам относятся разреженные массивы.
РАЗРЕЖЕННЫЕ МАССИВЫ. Разреженный массив - массив, большинство элементов которого равны между собой, так что хранить в памяти достаточно лишь небольшое число значений отличных от основного (фонового) значения остальных элементов.
МАССИВЫ С МАТЕМАТИЧЕСКИМ ОПИСАНИЕМ МЕСТОПОЛОЖЕНИЯ НЕФОНОВЫХ ЭЛЕМЕНТОВ. К данному типу массивов относятся массивы, у которых местоположения элементов со значениями, отличными от фонового, могут быть математически описаны, т. е. в их расположении есть какая-либо закономерность.
РАЗРЕЖЕННЫЕ МАССИВЫ СО СЛУЧАЙНЫМ РАСПОЛОЖЕНИЕМ ЭЛЕМЕНТОВ. К данному типу массивов относятся массивы, у которых местоположения элементов со значениями отличными от фонового, не могут быть математически описаны, т. е. в их расположении нет какой-либо закономерности.