Медианой Ме называют такое значение признака, которое приходится на середину ранжированного ряда и делит его на две равные по числу единиц части. Таким образом, в ранжированном ряду распределения одна половина ряда имеет значения признака, превышающие медиану, другая – меньше медианы.
Медиану используют вместо средней арифметической, когда крайние варианты ранжированного ряда (наименьшая и наибольшая) по сравнению с остальными оказываются чрезмерно большими или чрезмерно малыми.
В дискретном вариационном ряду, содержащем нечетное число единиц, медиана равна варианте признака, имеющей номер 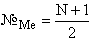 :
:
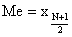 ,
,
где N – число единиц совокупности.
В дискретном ряду, состоящем из четного числа единиц совокупности, медиана определяется как средняя из вариант, имеющих номера 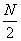 и
и 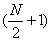 :
:
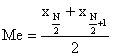 .
.
В распределении рабочих по стажу работы медиана равна средней из вариант, имеющих в ранжированном ряду номера 10 : 2 = 5 и 10 : 2 + 1 = 6. Варианты пятого и шестого признака равны 4 годам, таким образом
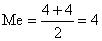 года
года
При вычислении медианы в интервальном ряду сначала находят медианный интервал, (т. е. содержащий медиану), для чего используют накопленные частоты или частости. Медианным является интервал, накопленная частота которого равна или превышает половину всего объема совокупности. Затем значение медианы рассчитывается по формуле:
 ,
,
где 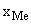 – нижняя граница медианного интервала;
– нижняя граница медианного интервала;
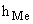 – ширина медианного интервала;
– ширина медианного интервала;
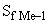 – накопленная частота интервала, предшествующего медианному;
– накопленная частота интервала, предшествующего медианному;
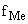 – частота медианного интервала.
– частота медианного интервала.
Рассчитаем медиану ряда распределения рабочих по размеру зарплаты (см. лекцию «Сводка и группировка статистических данных»).
Медианным является интервал заработной платы 800-900 грн., поскольку его кумулятивная частота равна 17, что превышает половину суммы всех частот (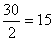 ). Тогда
). Тогда
Ме=800+100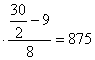 грн.
грн.
Полученное значение говорит о том, половина рабочих имеют заработную плату ниже 875 грн., но это выше среднего ее размера.
Для определения медианы можно вместо кумулятивных частот 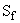 использовать кумулятивные частости
использовать кумулятивные частости 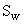 .
.
Медиана, как и мода, не зависит от крайних значений вариант, поэтому также применяется для характеристики центра в рядах распределения с неопределенными границами.
Свойство медианы:сумма абсолютных величин отклонений вариант от медианы меньше, чем от любой другой величины (в том числе и от средней арифметической):
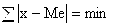
Это свойство медианы используется на транспорте при проектировании расположения трамвайных и троллейбусных остановок, бензоколонок, сборочных пунктов и т..д.
Пример. На шоссе длиной 100 км расположено 10 гаражей. Для проектирования строительства бензоколонки были собраны данные о числе предполагаемых ездок на заправку по каждому гаражу.
Таблица 2 – Данные о количестве ездок на заправку по каждому гаражу.
Километр шоссе, на котором расположен гараж |
7 |
26 |
28 |
37 |
40 |
46 |
60 |
78 |
86 |
92 |
Всего ездок |
Проектируемое число ездок |
10 |
15 |
5 |
20 |
5 |
25 |
15 |
30 |
10 |
65 |
200 |
Нужно поставить бензоколонку так, чтобы общий пробег автомашин на заправку был наименьшим.
Вариант 1. Если бензоколонку поставить в середине шоссе, т. е. на 50-ом километре (центр диапазона изменения признака), то пробеги с учетом числа ездок составят:
а) в одном направлении:
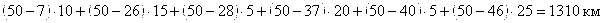 ;
;
б) в противоположном:
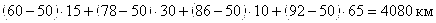 ;
;
в) общий пробег в оба направления: 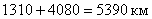 .
.
Вариант 2. Если бензоколонку поставить на среднем участке шоссе, определенном по формуле средней арифметической с учетом числа ездок:
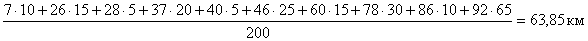
Тогда пробеги составят:
а) в одном направлении:


б) в противоположном:
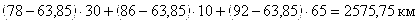 ;
;
в) общий пробег в оба направления, равный 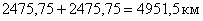 меньше, чем в первом варианте на 438,5 км.
меньше, чем в первом варианте на 438,5 км.
Вариант 3. Если поставить бензоколонку на 78-м километре, что будет соответствовать медиане по количеству ездок (накопленное число ездок для 60 км – 95, для 78 км – 125).
Тогда пробеги составят:
а) в одном направлении:

б) в противоположном:
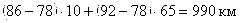 ;
;
в) общий пробег: 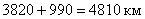 , меньше общих пробегов, рассчитанных по предыдущим вариантам.
, меньше общих пробегов, рассчитанных по предыдущим вариантам.
Таким образом, медиане соответствует наилучший результат, т. е. минимальный общий пробег.
Медиану можно определить графически, по кумуляте (см. лекцию «Сводка и группировка статистических данных»). Для этого последнюю ординату, равную сумме всех частот или частостей, делят пополам. Из полученной точки восстанавливают перпендикуляр до пересечения с кумулятой. Абсцисса точки пересечения и дает значение медианы.

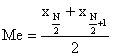 .
. ,
,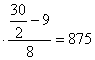 грн.
грн.